 por CarolMarques » Sáb Fev 23, 2013 13:40
por CarolMarques » Sáb Fev 23, 2013 13:40
Olá,
Tem duas integrais que eu não consegui resolver , a primeira:
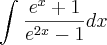
A primeira coisa que eu fiz foi simplifica a função ficando assim;
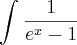
Dai eu tentei Integrar por partes substituindo
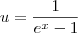
e dv=dx
A Segunda Integral q eu não consegui resolver foi essa daqui:
![\int_{}^{} \frac{1}{{x}^{3}}\sqrt[]{1 + \frac{1}{2x}} dx \int_{}^{} \frac{1}{{x}^{3}}\sqrt[]{1 + \frac{1}{2x}} dx](/latexrender/pictures/68f2dbf77eea58693ba7b5fb7ba4d514.png)
Essa eu não sei nem como começar.Seria uma integral por partes tendo como dv =1/x³dx e u= ao restante?
-
CarolMarques
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qui Mai 03, 2012 20:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por e8group » Sáb Fev 23, 2013 14:09
por e8group » Sáb Fev 23, 2013 14:09
Boa tarde . Usando a expressão fatorada que vc achou,somando-se

no numerador dela (note que 0 é o elemento neutro da adição ) ,
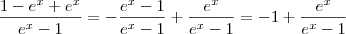
Observe que
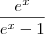
é extamemte a derivada da expressão
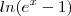
não é verdade ?
tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida no exercícios de calculo II
por 1marcus » Dom Abr 26, 2020 16:32
- 2 Respostas
- 5171 Exibições
- Última mensagem por adauto martins

Sáb Mai 02, 2020 14:57
Cálculo: Limites, Derivadas e Integrais
-
- Duvida em alguns exercícios de potenciação
por GiovaniF » Ter Mar 19, 2013 14:14
- 1 Respostas
- 1475 Exibições
- Última mensagem por timoteo

Ter Mar 19, 2013 21:51
Álgebra Elementar
-
- [duvida]Onde achar listas de exercicios de matematica
por UFSC » Qui Jun 23, 2016 07:53
- 2 Respostas
- 7138 Exibições
- Última mensagem por LuizAquino

Sáb Out 08, 2016 16:13
Assuntos Gerais ou OFF-TOPIC
-
- [Álgebra I, exercicios] Exercicios que estão sem resolução.
por vitorullmann » Ter Mar 05, 2013 21:26
- 0 Respostas
- 3296 Exibições
- Última mensagem por vitorullmann

Ter Mar 05, 2013 21:26
Álgebra Elementar
-
- EXERCÍCIOS.
por marcowrelio » Ter Dez 09, 2008 17:52
- 1 Respostas
- 5058 Exibições
- Última mensagem por Neperiano

Sex Set 16, 2011 19:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
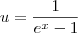
![\int_{}^{} \frac{1}{{x}^{3}}\sqrt[]{1 + \frac{1}{2x}} dx \int_{}^{} \frac{1}{{x}^{3}}\sqrt[]{1 + \frac{1}{2x}} dx](/latexrender/pictures/68f2dbf77eea58693ba7b5fb7ba4d514.png)


 no numerador dela (note que 0 é o elemento neutro da adição ) ,
no numerador dela (note que 0 é o elemento neutro da adição ) , 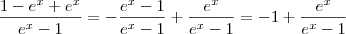
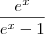 é extamemte a derivada da expressão
é extamemte a derivada da expressão 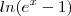 não é verdade ?
não é verdade ?
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.