Olá
Santtus,
consegui resolver, no entanto, não sei se é a forma mais simples! Segue:
Consideremos o prédio mais ALTO sendo:

Meio:

Baixo:

Do enunciado temos:

Apenas com essas informações, e que são ímpares, não somos capazes de determinar tais valores, por isso, devemos encontrar uma condição entre

e

, isto é, entre o prédio do meio e o mais baixo.
Vamos lá:
- sabemos que

, e, que
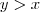
, então temos 3 possibillidades, veja:
Ou,
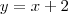
Ou,

Ou,
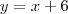
Por quê estou somando

a um valor par? Para que satisfaçam a condição de serem ímpares. Qualquer número
ímpar somado a um número
par resulta em ímpar!!
Vamos testar a primeira, ou seja:
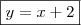
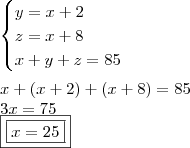
Noossa, que sorte, e, de primeira! [risos].
Agora é só encontrar as demais variáveis e fazer o que se pede!
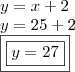
E,

Por fim,
Baixo:2 + 5 =
7Meio:2 + 7 =
9Alto:3 + 3 =
6





 , e, que
, e, que 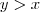 , então temos 3 possibillidades, veja:
, então temos 3 possibillidades, veja: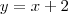

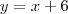
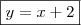
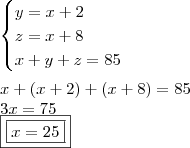
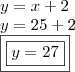





 .
.



