 por laura_biscaro » Seg Fev 18, 2013 19:19
por laura_biscaro » Seg Fev 18, 2013 19:19
O conjunto verdade da equação:

+
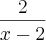
=
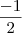
é:
a) {-2}
b) {-2;-1}
c) {2;-1}
d) não existe
e) {-2;1}
-
laura_biscaro
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Fev 18, 2013 19:05
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Seg Fev 18, 2013 20:16
por Cleyson007 » Seg Fev 18, 2013 20:16
Boa noite Laura!
Seja bem-vinda ao Ajuda Matemática!
Basta tirar o M.M.C e seguir o procedimento que é de costume (divida no denominador e multiplique no numerador).
Tenta aí, qualquer coisa me informe

Att,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por laura_biscaro » Seg Fev 18, 2013 21:36
por laura_biscaro » Seg Fev 18, 2013 21:36
olá! obrigada, esse site veio em boa hora haha
enfim, pergunta meio estúpida agora mas, como se tira o MMC de x mesmo? eu esqueci completamente :/
obrigada

-
laura_biscaro
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Fev 18, 2013 19:05
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Seg Fev 18, 2013 22:08
por Cleyson007 » Seg Fev 18, 2013 22:08
Laura, acompanhe a resolução:
O MMC --> 2(x+2)(x-2).
Multiplicando a expressão por 2(x+2)(x-2):
(x+2)².(x-2) +2.2(x+2)=-1.(x+2)(x-2)
(x+2). [x² - 4 +4]=(x+2)[2-x]
x diferente de -2
[x² -4 +4]= 2 - x
x² + x - 2 = 0
S = -1
P = -2
x' = 1 e x" = -2
Como x diferente de -2,
---> S={1}
Qualquer coisa me avise, ok?

Bons estudos!
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por laura_biscaro » Seg Fev 18, 2013 22:40
por laura_biscaro » Seg Fev 18, 2013 22:40
aaah agora consegui! S = {-2;1}
muito simples, não sei como não pensei nisso antes. muito obrigada

Boa Noite!
-
laura_biscaro
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Fev 18, 2013 19:05
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Seg Fev 18, 2013 23:02
por Cleyson007 » Seg Fev 18, 2013 23:02
Que bom que entendeu Laura

Sempre que precisar, poste as dúvidas aqui no fórum. Ok?
Att,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Inequação e Conjunto Verdade
por Cleyson007 » Ter Mai 11, 2010 23:30
- 1 Respostas
- 3998 Exibições
- Última mensagem por MarceloFantini

Qua Mai 12, 2010 13:55
Funções
-
- Tabela Verdade
por Dan » Seg Mar 07, 2011 01:08
- 6 Respostas
- 5672 Exibições
- Última mensagem por Dan

Seg Mar 07, 2011 21:21
Álgebra Elementar
-
- CONSTRUIR TABELA VERDADE
por mayke Paiva » Qui Mar 29, 2012 17:28
- 0 Respostas
- 2500 Exibições
- Última mensagem por mayke Paiva

Qui Mar 29, 2012 17:28
Álgebra Elementar
-
- [FUNÇÃO PAR E ÍMPAR] Mostrar uma verdade absoluta
por samifel » Qui Abr 12, 2012 17:07
- 1 Respostas
- 1921 Exibições
- Última mensagem por MarceloFantini

Qui Abr 12, 2012 19:25
Funções
-
- Conjunto vazio está dentro de outro conjunto vazio?
por JDomingos » Dom Jul 20, 2014 07:41
- 1 Respostas
- 2223 Exibições
- Última mensagem por DanielFerreira

Dom Jul 20, 2014 12:14
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 +
+ 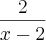 =
= 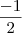 é:
é:
 +
+ 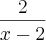 =
= 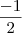 é:
é:









 .
.



