 por santtus » Sáb Fev 16, 2013 17:41
por santtus » Sáb Fev 16, 2013 17:41
Numa sorveteria são oferecidos 8 sabores diferentes de sorvete e 4 tipos de cobertura. Ao preparar um
“banana-split”, um cliente deseja escolher 3 bolas de sabores diferentes e 2 tipos de cobertura. De quantas
maneiras esse cliente poderá preparar o “banana-split”, considerando que uma das bolas deve ser de
chocolate, seu sabor favorito?

-
santtus
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Fev 08, 2013 02:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Rafael16 » Sáb Fev 16, 2013 18:31
por Rafael16 » Sáb Fev 16, 2013 18:31
Temos 8 sabores de sorvete e devemos escolher 3, mas um dos 3 sabores deve ser de chocolate.
Devemos então fazer a combinação
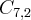
(Tirei o sabor de chocolate e sobrou 7 sabores e vou fazer a combinação desses sabores de dois em dois, para depois acrescentar o sabor de chocolate em cada uma das combinações ficando assim com 3 sabores)

-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por santtus » Sáb Fev 16, 2013 18:51
por santtus » Sáb Fev 16, 2013 18:51
obrigado rafael ....ja havia conseguido mas msm assim agradeço... agora so resta essa aqui que nao ta batendo o resultado
A banana-split é uma sobremesa composta por 3 bolas de sorvete. Numa sorveteria que dispõe de 8 sabores,
de quantas maneiras uma pessoa poderá comprar essa sobremesa?
-
santtus
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Fev 08, 2013 02:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Rafael16 » Sáb Fev 16, 2013 19:00
por Rafael16 » Sáb Fev 16, 2013 19:00
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por santtus » Qua Fev 20, 2013 01:20
por santtus » Qua Fev 20, 2013 01:20
amigo rafael aqui diz que o resultado e 120. e agora?
-
santtus
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Fev 08, 2013 02:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sex Fev 22, 2013 00:05
por DanielFerreira » Sex Fev 22, 2013 00:05
Santtus,
uma questão por tópico, ok?!
O
Rafael16 cometeu um pequeno lapso (acredito que o erro de digitação tenha proporcionado isso, uma vez que, o raciocínio está correto).
Segue:
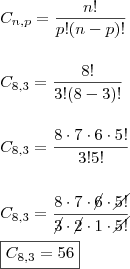
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Análise Combinatória
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ANALISE COMBINATÓRIA - AJUDA URGENTE!
 por adriano_casp » Sex Abr 09, 2010 16:39
por adriano_casp » Sex Abr 09, 2010 16:39
- 2 Respostas
- 2297 Exibições
- Última mensagem por estudandoMat

Sex Abr 09, 2010 20:07
Estatística
-
- [Análise Combinatória] Ajuda Urgente
 por marcelojs » Ter Jun 11, 2013 13:04
por marcelojs » Ter Jun 11, 2013 13:04
- 2 Respostas
- 2126 Exibições
- Última mensagem por marcelojs

Qua Jun 12, 2013 22:03
Análise Combinatória
-
- [Análise Combinatória] Ajuda Urgente
por marcelojs » Qua Jun 12, 2013 09:26
- 1 Respostas
- 1610 Exibições
- Última mensagem por marcelojs

Sex Jun 14, 2013 23:11
Análise Combinatória
-
- [Análise Combinatória] Ajuda Urgente
 por marcelojs » Qua Jun 12, 2013 09:34
por marcelojs » Qua Jun 12, 2013 09:34
- 0 Respostas
- 1115 Exibições
- Última mensagem por marcelojs

Qua Jun 12, 2013 09:34
Análise Combinatória
-
- Analise combinatória (AFA) Ajuda-me por favor
por George005 » Sáb Set 06, 2014 01:10
- 3 Respostas
- 3895 Exibições
- Última mensagem por DanielFerreira

Seg Set 08, 2014 19:36
Análise Combinatória
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




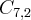 (Tirei o sabor de chocolate e sobrou 7 sabores e vou fazer a combinação desses sabores de dois em dois, para depois acrescentar o sabor de chocolate em cada uma das combinações ficando assim com 3 sabores)
(Tirei o sabor de chocolate e sobrou 7 sabores e vou fazer a combinação desses sabores de dois em dois, para depois acrescentar o sabor de chocolate em cada uma das combinações ficando assim com 3 sabores)




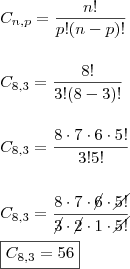

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
