RESOLVA ESSA QUESTÃO DO CONCURSO CFOPM/BA
QUESTÃO43) Em um dia de grande movimentação em uma delegacia de polícia, o tempo médio e o tempo mediano de espera para atendimento de um grupo de 10 pessoas foram, ambos, iguais a 12 minutos.
Sabendo-se que o conjunto ordenado de valores 4,5,5,9,a,14,16,18,b,21 corresponde ao tempo de espera, em minutos, de cada uma dessas pessoas, pode-se concluir que b - a é igual a
01) 9
02) 8
03) 7
04) 6
05)5
RESPOSTA DO GABARITO 02)8


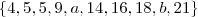
 e
e 

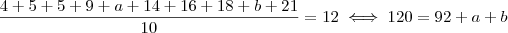 .
. certo ? Então,somando-se
certo ? Então,somando-se 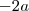 em ambos membros da igualdade ,
em ambos membros da igualdade ,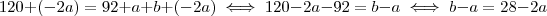
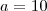 concluímos que
concluímos que 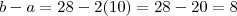


 .
.
 :
: