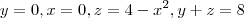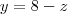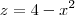por Aniinha » Qua Fev 13, 2013 17:45
por Aniinha » Qua Fev 13, 2013 17:45
Oi gente, sou nova aqui no fórum então se algo estiver errado me orientem

Então ... to com uma dúvida, em integral tripla. Eu não sei como achar os intervalos de integração e como ficaria num gráfico essa seguinte integral :

onde T é delimitada por
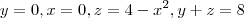
Grata ^^
-
Aniinha
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Fev 13, 2013 17:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de automação
- Andamento: cursando
 por young_jedi » Qui Fev 14, 2013 12:12
por young_jedi » Qui Fev 14, 2013 12:12
das equações temos que
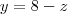
como ela é delimintado por x=0 e
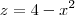
então integral em x vai de 0 ate 2
portanto a integral fica

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Aniinha » Qui Fev 14, 2013 23:03
por Aniinha » Qui Fev 14, 2013 23:03
No enunciado da questão, esqueci de tmb por z=0, muda alguma coisa?
Tentei ir por esse seu intervalo aí, e não cheguei na resposta ! :/
-
Aniinha
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Fev 13, 2013 17:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de automação
- Andamento: cursando
 por young_jedi » Sex Fev 15, 2013 10:33
por young_jedi » Sex Fev 15, 2013 10:33
não, na verdade eu fiz imaginando que z=0 mesmo
so confirme se x=0 e y=0
e se tiver como colocar a resposta ajudaria
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral Tripla
por Cleyson007 » Qua Mai 16, 2012 11:41
- 2 Respostas
- 2082 Exibições
- Última mensagem por LuizAquino

Sex Mai 18, 2012 20:14
Cálculo: Limites, Derivadas e Integrais
-
- Integral tripla
por DanielFerreira » Dom Jun 10, 2012 19:27
- 1 Respostas
- 1696 Exibições
- Última mensagem por Russman

Seg Jun 11, 2012 00:39
Cálculo: Limites, Derivadas e Integrais
-
- INTEGRAL TRIPLA
por Garota nerd » Qua Jun 27, 2012 17:40
- 4 Respostas
- 3126 Exibições
- Última mensagem por Garota nerd

Qui Jun 28, 2012 01:28
Cálculo: Limites, Derivadas e Integrais
-
- Integral tripla
por DanielFerreira » Sáb Jul 07, 2012 13:00
- 2 Respostas
- 1877 Exibições
- Última mensagem por DanielFerreira

Dom Jul 08, 2012 13:01
Cálculo: Limites, Derivadas e Integrais
-
- Integral Tripla!
por samysoares » Sáb Nov 09, 2013 00:23
- 1 Respostas
- 1316 Exibições
- Última mensagem por Man Utd

Sex Nov 15, 2013 15:09
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 onde T é delimitada por
onde T é delimitada por 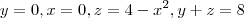


 onde T é delimitada por
onde T é delimitada por