 por edsongsrj » Qua Fev 13, 2013 21:39
por edsongsrj » Qua Fev 13, 2013 21:39
Aos senhores
Deste site excelente.
Alguns membros muito prestativos me responderam porem ainda nao conclui a duvida principal.
Como calcular a taxa de juro composto sem uso de calculadora. Por exemplo: raiz cubica de 1.0385?? Ou raiz sextupla de 1.0385??
O motivo é que estou estudando para Petrobras e cairam duas questoes pedindo para calcular a taxa juros composto sem uso de calculadora. Uma das questoes ja citei acima.
Nao encontrei até agora nenhuma apostila ou video explicando sem calculadora porem na prova tem que fazer sem calculadora. É possivel calcular resolver sem calculadora??
Por favor aguardo. Atenciosamente, Edson.
-
edsongsrj
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Fev 10, 2013 10:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por e8group » Qua Fev 13, 2013 23:16
por e8group » Qua Fev 13, 2013 23:16
Usando o seu exemplo
![\sqrt[3] = 1,0385 \sqrt[3] = 1,0385](/latexrender/pictures/f60e59a3444afb9d70f8909fa0a57df2.png)
.
Pense assim, qual valor que elevado a 3 resulta 1,0385 ,é extremamente difícil encontra exatamente este valor sem o uso da calculadora,mas podemos aproximar dele.
Suponha que
![x = \sqrt[3]{ 1,0385} \implies x^3 = 1,0385 \implies x^3 - 1,0385 = 0 x = \sqrt[3]{ 1,0385} \implies x^3 = 1,0385 \implies x^3 - 1,0385 = 0](/latexrender/pictures/415e476b76ec6bd03c429e8cf0633305.png)
e vamos considerar
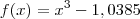
.
Vamos investigar :
Quando

,
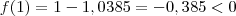
e
quando
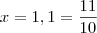
,
![f(1,1) = (1,1)^3 - 1,0385 = \frac{11^3}{10^3} - 1,0385 = \frac{11 \cdot 11^2 }{10^3} -1,0385 = \frac{(10 + 1)(121 )10 -10385}{10^4} = \frac{[1210 + 121]10 -10385 }{10^4} = \frac{13310 -10385}{10^4} = \frac{2925}{10000} = 0,2925 > 0 f(1,1) = (1,1)^3 - 1,0385 = \frac{11^3}{10^3} - 1,0385 = \frac{11 \cdot 11^2 }{10^3} -1,0385 = \frac{(10 + 1)(121 )10 -10385}{10^4} = \frac{[1210 + 121]10 -10385 }{10^4} = \frac{13310 -10385}{10^4} = \frac{2925}{10000} = 0,2925 > 0](/latexrender/pictures/1a5044bc3056f730d4ae79151e41297d.png)
. Como
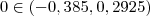
então ,
![1,1 > \sqrt[3]{ 1,0385} >1 1,1 > \sqrt[3]{ 1,0385} >1](/latexrender/pictures/fef461db4f628306757eeb546508eab1.png)
.
Poderíamos dizer que
![\sqrt[3]{ 1,0385} \approx 1,1 \sqrt[3]{ 1,0385} \approx 1,1](/latexrender/pictures/767e5e8de3d5b86d76c5b6973c821764.png)
Na verdade

.
Observação, ainda podemos obter aproximações mais eficientes ,basta tomar valores em
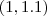
e verificar qual deles faz

se aproximar mais de zero .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- taxa juros composto sem calculadora
por edsongsrj » Qua Fev 13, 2013 12:14
- 1 Respostas
- 2132 Exibições
- Última mensagem por Cleyson007

Qua Fev 13, 2013 13:05
Matemática Financeira
-
- Juros Composto TaxA
por djeffersound » Qua Jun 23, 2010 19:39
- 0 Respostas
- 2191 Exibições
- Última mensagem por djeffersound

Qua Jun 23, 2010 19:39
Matemática Financeira
-
- Juros composto taxa
por djeffersound » Qua Jun 23, 2010 19:46
- 1 Respostas
- 3671 Exibições
- Última mensagem por Lucio Carvalho

Qua Jun 23, 2010 20:14
Matemática Financeira
-
- Juros simples, calcular taxa;
por elisamaria » Qua Mar 11, 2015 15:41
- 1 Respostas
- 8021 Exibições
- Última mensagem por Baltuilhe

Dom Mar 15, 2015 17:00
Matemática Financeira
-
- Calcular a taxa mensal de juros (gente me ajude por favor)!!
por vivi » Sáb Mai 10, 2014 18:57
- 0 Respostas
- 2120 Exibições
- Última mensagem por vivi

Sáb Mai 10, 2014 18:57
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![\sqrt[3] = 1,0385 \sqrt[3] = 1,0385](/latexrender/pictures/f60e59a3444afb9d70f8909fa0a57df2.png) .
. ![x = \sqrt[3]{ 1,0385} \implies x^3 = 1,0385 \implies x^3 - 1,0385 = 0 x = \sqrt[3]{ 1,0385} \implies x^3 = 1,0385 \implies x^3 - 1,0385 = 0](/latexrender/pictures/415e476b76ec6bd03c429e8cf0633305.png)
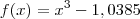 .
.  ,
, 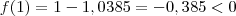 e
e 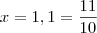 ,
, ![f(1,1) = (1,1)^3 - 1,0385 = \frac{11^3}{10^3} - 1,0385 = \frac{11 \cdot 11^2 }{10^3} -1,0385 = \frac{(10 + 1)(121 )10 -10385}{10^4} = \frac{[1210 + 121]10 -10385 }{10^4} = \frac{13310 -10385}{10^4} = \frac{2925}{10000} = 0,2925 > 0 f(1,1) = (1,1)^3 - 1,0385 = \frac{11^3}{10^3} - 1,0385 = \frac{11 \cdot 11^2 }{10^3} -1,0385 = \frac{(10 + 1)(121 )10 -10385}{10^4} = \frac{[1210 + 121]10 -10385 }{10^4} = \frac{13310 -10385}{10^4} = \frac{2925}{10000} = 0,2925 > 0](/latexrender/pictures/1a5044bc3056f730d4ae79151e41297d.png) . Como
. Como 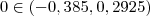
![1,1 > \sqrt[3]{ 1,0385} >1 1,1 > \sqrt[3]{ 1,0385} >1](/latexrender/pictures/fef461db4f628306757eeb546508eab1.png) .
. ![\sqrt[3]{ 1,0385} \approx 1,1 \sqrt[3]{ 1,0385} \approx 1,1](/latexrender/pictures/767e5e8de3d5b86d76c5b6973c821764.png)
 .
.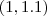 e verificar qual deles faz
e verificar qual deles faz  se aproximar mais de zero .
se aproximar mais de zero .

 .
.



