 por dexter » Ter Fev 12, 2013 15:58
por dexter » Ter Fev 12, 2013 15:58
Y = quantidade
X = reais
Sendo y = f(x)
f(250) = 180 e f ' (250) = 2
Interpretar
-
dexter
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Fev 04, 2013 10:49
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por DanielFerreira » Ter Fev 12, 2013 17:00
por DanielFerreira » Ter Fev 12, 2013 17:00
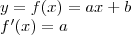
Então,

E,
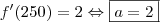
Calculemos

...
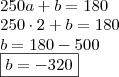
Logo,
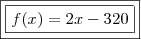
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por dexter » Ter Fev 12, 2013 17:10
por dexter » Ter Fev 12, 2013 17:10
Obrigado pela ajuda. A questão diz que Y = assinaturas do jornal e X = reais gastos em propaganda e quer uma interpretação. Significa então que essa última fórmula no post é o ponto de equilíbrio? (160 reais gastos equivalem a 250 assinaturas?)
-
dexter
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Fev 04, 2013 10:49
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por DanielFerreira » Ter Fev 12, 2013 17:27
por DanielFerreira » Ter Fev 12, 2013 17:27
Dexter,
ponha a questão completa!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por dexter » Ter Fev 12, 2013 17:31
por dexter » Ter Fev 12, 2013 17:31
O número de novas assinaturas de um jornal, y, em um mês é função da quantia, x, em reais, gasta em propaganda nesse mês, assim, y = f(x).
A) interprete as informações: f(250) = 180 e f ' (250) = 2.
Segundo ele "o cálculo está feito, falta interpretar"-
Agradeço!
-
dexter
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Fev 04, 2013 10:49
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por dexter » Qua Fev 13, 2013 09:35
por dexter » Qua Fev 13, 2013 09:35
Alguem poderia ajudar, por favor?
Não consegui responder.
-
dexter
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Fev 04, 2013 10:49
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5576 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4591 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5751 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- +uma função das trevas.ajuda aew!(função par mas heim!?)
por Fabricio dalla » Dom Fev 27, 2011 16:12
- 2 Respostas
- 3488 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 09:17
Funções
-
- [FUNÇÃO] Não consigo achar a fórmula da função
por LAZAROTTI » Qui Set 27, 2012 00:06
- 1 Respostas
- 2957 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 07:13
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


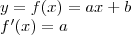

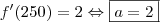
 ...
...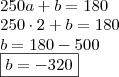
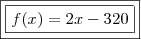






 .
.
 :
: