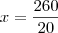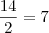Tenho 20 moedas. Algumas delas são de 20 centavos e outras de 10 centavos. Se as moedas de 10 centavos que eu tenho fossem as de 20, e as de 20 fossem as de 10, eu teria 60 centavos a mais do que eu tenho agora. Quantas moedas de 10 e quantas moedas de 20 eu tenho?
SOLUÇÃO POR SISTEMAS DE EQUAÇÕES
x + y = 20 => x = 20 - y
10x + 20y = 20x + 10y - 60
10(20 - y) + 20y = 20(20 - y) + 10y - 60
200 - 10y + 20y = 400 - 20y + 10y -60
10y + 10y = 400 - 200 - 60
y = 140 / 20 => y = 7
x = 20 - 7 => x = 13
Há alguma solução sem uso de sistemas??