Calcule o domínio máximo D da seguinte função:
Observação: A notação f:D
 X -> Y indica uma função f:D -> Y, onde D
X -> Y indica uma função f:D -> Y, onde D  X
Xf:D
 R -> R, f(x) = 1/ ?x² - 1
R -> R, f(x) = 1/ ?x² - 1___________________________________________________________________________________________
sabendo que o denominador deve ser diferente de 0 , devo descobrir a raiz de x² - 1 = 0 e sabendo que
x² - 1 está contido em uma raiz, devo considerar x² - 1 > 0
x² = 1
x = ?1
x = -1 e 1
D = {x
 R / 1 < x < - 1}
R / 1 < x < - 1}Estou correto no procedimento e resultado? Há um jeito mais simples de resolver o exercício?
Obrigado


 estar definida somente quando
estar definida somente quando  e
e 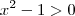 . Ou seja ,
. Ou seja , 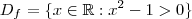 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)