 por klueger » Ter Fev 05, 2013 15:42
por klueger » Ter Fev 05, 2013 15:42
Olá. Tenho uma integral que não cheguei a solução:

'
Dica dela: usar "x.x²" no começo, primeiro fazer Substituição e depois por Partes.
-
klueger
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Fev 03, 2013 15:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por e8group » Ter Fev 05, 2013 20:34
por e8group » Ter Fev 05, 2013 20:34
Façamos então a dica , temos :

.
Sendo
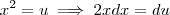
.Substituindo ,obtemos :
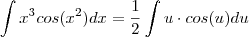
Tente concluir.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral por Substituição e por Partes
 por Jhenrique » Sáb Set 15, 2012 14:59
por Jhenrique » Sáb Set 15, 2012 14:59
- 23 Respostas
- 31219 Exibições
- Última mensagem por Jhenrique

Qua Set 26, 2012 21:26
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] SUBSTITUIÇÃO E POR PARTES
por FERNANDA_03 » Sex Mar 29, 2013 14:00
- 1 Respostas
- 1809 Exibições
- Última mensagem por young_jedi

Sex Mar 29, 2013 16:08
Cálculo: Limites, Derivadas e Integrais
-
- Integral por substituição ou por partes.
por Sobreira » Sáb Jul 20, 2013 15:03
- 1 Respostas
- 2705 Exibições
- Última mensagem por young_jedi

Sex Jul 26, 2013 20:42
Cálculo: Limites, Derivadas e Integrais
-
- [Integral por partes e substituição]
por vergilxdante » Seg Mar 31, 2014 15:28
- 0 Respostas
- 1830 Exibições
- Última mensagem por vergilxdante

Seg Mar 31, 2014 15:28
Cálculo: Limites, Derivadas e Integrais
-
- Integral por partes ou substituição
por Flavio Casaes » Dom Fev 08, 2015 00:20
- 8 Respostas
- 6706 Exibições
- Última mensagem por nakagumahissao

Seg Fev 09, 2015 12:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 .
. 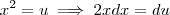 .Substituindo ,obtemos :
.Substituindo ,obtemos : 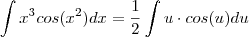


 .
.
 :
: