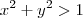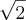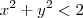Olá, meu nome é Marlon, eu passei por varios problemas no ensino médio e acabei por concluir pelo enem e sem base nenhuma, depois disso acabei por entrar pra engenharia de computação e até tenho conseguido entender calculo e outras matérias, mas geometria analítica realmente parece ser minha kriptonita.
por exemplo: Determine os pontos da interseção da reta y = 2x com o círculo x² + y² = 1.
Essa questão, que pelo menos me parece simples, eu não sei como iniciar a resolver. Vocês teriam alguma dica sobre como resolver meu problema?




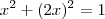

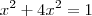
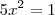
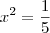
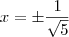
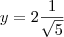
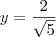
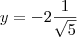
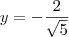
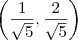
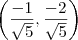
 , porem tenho varias outras duvidas, por exemplo, no caso de exboçamento de gráfico, como eu faço?
, porem tenho varias outras duvidas, por exemplo, no caso de exboçamento de gráfico, como eu faço?