quando calculo eu faço assim...
cos f(x) = 2 . (x/2 + 3) -->
 -->
-->S=[-7, -5].
porem a resposta do livro é realizada como se o dois nao multiplicasse com (cos f(x) = 2 . (x/2 + 3)).
ficando assim:
cosf(x) = x/2 + 3 -->
 -->
-->S= [-8, -4].
parece-me que quando procura-se o dominio o dois nao tem relevancia. nao influencia no resultado final.
mas, verifique que o mesmo nao ocorre com a imagem; donde o dois ou qualquer n tem importancia no resultado final...
alguem poderia dizer se estou certo e o porque da aparente exclusão do dois no caso do dominio?


 como composição de duas outras funções multiplicada por uma função constante .
como composição de duas outras funções multiplicada por uma função constante .  e
e  funções definidas por
funções definidas por 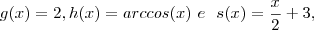
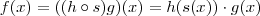 .
.  .
.  e
e ![D_{h\circ s} = D_h \cap Im_s = [-1,1] D_{h\circ s} = D_h \cap Im_s = [-1,1]](/latexrender/pictures/3d9a9e6b7270822bd6c9561b1a375578.png) .Desta forma ,
.Desta forma , ![D_f = D_{h\circ s} \cap D_g = [-1,1] D_f = D_{h\circ s} \cap D_g = [-1,1]](/latexrender/pictures/27053f5550c66bcc19c2c651d9496b49.png) .
. é cosntante, segue que :
é cosntante, segue que : ![s(x) \in [-1,1] s(x) \in [-1,1]](/latexrender/pictures/3fe2cf7194bc140437c37079dd518b15.png) .
.  . Espero que ajude !
. Espero que ajude !![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)