 por sadzinski » Qui Jan 10, 2013 11:42
por sadzinski » Qui Jan 10, 2013 11:42
O lucro que uma empresa obtém, vendendo dois tipos de produtos A e B, é dado por f(x,y)= 600 - 2x² - 4y² - 3xy - 2x² - 2,5y² , em que x e y são as quantidades vendidas.Obtenha os valores de x e y que maximizam o lucro.
Nestes problemas de otimização, eu acabo tendo dificuldades em entender o que o problema pede.
Ex. neste exercício, acredito eu que devo começar derivando parcialmente a função, mas e depois disso?
Eu imagino que devo isolar as variáveis para encontrar o resultado.
Se puderem me indicar um caminho para iniciar estes tipos de problema.
Obrigado.
-
sadzinski
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jan 01, 2013 16:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia em Fabricação Mecânica
- Andamento: cursando
 por young_jedi » Qui Jan 10, 2013 20:36
por young_jedi » Qui Jan 10, 2013 20:36
os pontos de maximo e minimo se localizam onde as derivadas são iguais a zero.
calcule as derivadas parciais e iguale elas a 0
assim voce tera um sistema de equaçoes com duas equações, então resolvendo este sistema voce encontra os valores de x e y
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por sadzinski » Sex Jan 11, 2013 08:29
por sadzinski » Sex Jan 11, 2013 08:29
Se possível de uma conferida.
Ficou uma duvida no seguinte ponto:
- Quando devo igualar a 0 a equação?
- Quando se deve somar as derivadas parciais?
- Anexos
-
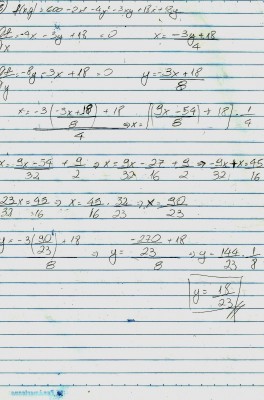
- Resolução do exercício
-
sadzinski
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jan 01, 2013 16:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia em Fabricação Mecânica
- Andamento: cursando
 por young_jedi » Sex Jan 11, 2013 11:29
por young_jedi » Sex Jan 11, 2013 11:29
eu dei uma olhada e acho que esta certo
com relação as duvidas
voce calcula a derivada parcial com relação a x igula a zero, assim voce vai ter uma equação
depois voce calcula a derivada parcial com relação a y e iguala a zero, voce vai ter outra equação
com as duas equações voce vai ter um sistema de equações, que voce pode resolver da maneira que voce preferir. Do jeito que voce fez, voce utilizou o metodo da substituição onde voce isola uma incognita em uma equação e substitui na outra
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Aplicação e Otimização de derivadas] Custo, receita e lucro
por ricael » Ter Out 23, 2012 11:21
- 2 Respostas
- 4552 Exibições
- Última mensagem por ricael

Ter Out 23, 2012 16:25
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo do lucro com função do segundo grau
por chenz » Qua Jun 02, 2010 10:07
- 2 Respostas
- 7356 Exibições
- Última mensagem por chenz

Qua Jun 09, 2010 11:00
Funções
-
- Otimização Calculo 2
 por sadzinski » Qua Jan 02, 2013 18:55
por sadzinski » Qua Jan 02, 2013 18:55
- 6 Respostas
- 4498 Exibições
- Última mensagem por young_jedi

Qui Jan 10, 2013 10:39
Cálculo: Limites, Derivadas e Integrais
-
- Otimização calculo 2
por sadzinski » Qua Jan 09, 2013 17:52
- 0 Respostas
- 742 Exibições
- Última mensagem por sadzinski

Qua Jan 09, 2013 17:52
Cálculo: Limites, Derivadas e Integrais
-
- Otimização calculo 2 ( Um edifício )
por sadzinski » Ter Jan 15, 2013 08:47
- 1 Respostas
- 2991 Exibições
- Última mensagem por young_jedi

Ter Jan 15, 2013 15:04
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
