Potenciação

por **lucas77** » Qua Jan 09, 2013 20:18

Olá!

A minha dúvida é quanto a esta regra da potenciação. Não sei como resolvê-la e gostaria que vocês pudessem me explicar esta regra por favor.
${(-a,a)}^{-\frac{a}{a}}$

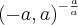
Por exemplo:
${(-0,1)}^{-\frac{1}{3}}$

Como resolver isto?

Obrigado!

por **Russman** » Qua Jan 09, 2013 22:05

Em geral, os números decimais podem ser expressos como frações , chamadas de frações geratrizes. É bem verdade que os decimais se devem a uma motivação fracionária. Assim, basta que você escreva o número em forma de fração e aplique a propriedade exponencial para esta. Uma fração elevada a um certo número equivale a você elevar o numerador e o denominador a este numero e , disto, obter o resultado.

Vou fazer um exemplo: $(-0,3)^{-\frac{1}{4}}$

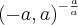
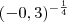
Como eu disse podemos escrever $0,3 = 3 . 0,1 = 3. \frac{1}{10} = \frac{3}{10}$ , de forma que

$0,3^{-\frac{1}{4}} = \left ( \frac{3}{10} \right )^{-\frac{1}{4}} = \frac{3^{-\frac{1}{4}}}{10^{-\frac{1}{4}}}$ .

Agora, lembre-se que

$a ^{-x} = \frac{1}{a^x}$ , $a \neq 0$

e que

$a^{\frac{b}{c}} = \sqrt[c]{a^b}$ .

Assim, $3^{-\frac{1}{4}} = \frac{1}{3^{\frac{1}{4}}} = \frac{1}{\sqrt[4]{3}}$ e $10^{-\frac{1}{4}} = \frac{1}{10^{\frac{1}{4}}} = \frac{1}{\sqrt[4]{10}}$ . Portanto,

$0,3^{-\frac{1}{4}} = \frac{3^{-\frac{1}{4}}}{10^{-\frac{1}{4}}} =$
$= \frac{\frac{1}{\sqrt[4]{3}}}{\frac{1}{\sqrt[4]{10}}} = \frac{1}{\sqrt[4]{3}}.\frac{\sqrt[4]{10}}{1} = \frac{\sqrt[4]{10}}{\sqrt[4]{3}}$

Agora basta racionalizar a fração.

Potenciação

Potenciação

Potenciação

Re: Potenciação

Quem está online