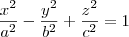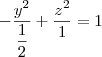Cônicas e quádricas

[Danilo]

Reduzir a equação de forma a identificar a quádrica que ela representa e faça um esboço do seu gráfico.



Bom, eu sei que cada quádrica (elipsoide, hiperboloide etc) tem a sua equação correspondente. Mas eu não consigo simplificar de forma a chegar em uma das equações... na verdade como são várias equações eu não sei de que ponto partir. E para piorar, eu não sei como fazer um gráfico porque o gráfico é desenhado no. Grato a quem puder dar uma luz.

[LuizAquino]

Reduzir a equação de forma a identificar a quádrica que ela representa e faça um esboço do seu gráfico.

Bom, eu sei que cada quádrica (elipsoide, hiperboloide etc) tem a sua equação correspondente. Mas eu não consigo simplificar de forma a chegar em uma das equações... na verdade como são várias equações eu não sei de que ponto partir.

Vamos reescrever a equação da seguinte forma:



Desse modo, podemos perceber que ela tem o formato do tipo:



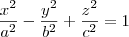
Como você já deve ter estudado, uma equação deste tipo representa um hiperboloide de uma folha (detalhe: segundo as novas regras do acordo ortográfico da língua portuguesa, a palavra correta é "hiperboloide" e não mais "hiperbolóide" como era antes).

E para piorar, eu não sei como fazer um gráfico porque o gráfico é desenhado no .

Você pode seguir um roteiro básico:
1) determine a interseção com o plano xy (ou seja, z = 0);
2) determine a interseção com o plano xz (ou seja, y = 0);
3) determine a interseção com o plano yz (ou seja, x = 0).

Vejamos a aplicação desse roteiro.

Passo 1)

Considerando o plano xy (ou seja, z = 0), a equação da superfície é simplificada para:



Agora pense um pouco: o que esta equação representa no plano? Ora, ela representa uma hipérbole com vértices sobre o eixo x. A figura abaixo ilustra esta hipérbole no sistema xyz.

intersecao_xy.png (4.27 KiB) Exibido 5071 vezes

Passo 2)

Considerando o plano xz (ou seja, y = 0), a equação da superfície é simplificada para:



Agora pense um pouco: o que esta equação representa no plano? Ora, ela representa uma elipse com eixo maior sobre o eixo z. A figura abaixo ilustra esta elipse no sistema xyz.

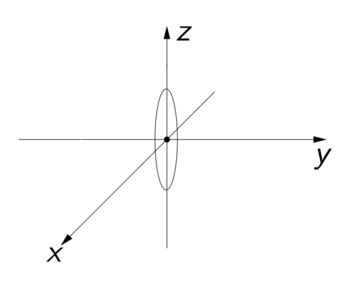
intersecao_xz.png (4.25 KiB) Exibido 5071 vezes

Passo 3)

Considerando o plano yz (ou seja, x = 0), a equação da superfície é simplificada para:



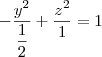
Agora pense um pouco: o que esta equação representa no plano? Ora, ela representa uma hipérbole com vértices sobre o eixo z. A figura abaixo ilustra esta hipérbole no sistema xyz.

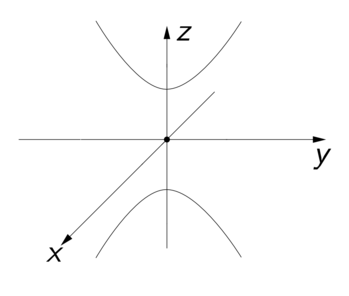
intersecao_yz.png (5.59 KiB) Exibido 5071 vezes

Usando agora tudo que discutimos até aqui, temos que a figura abaixo ilustra o hiperboloide de uma folha.

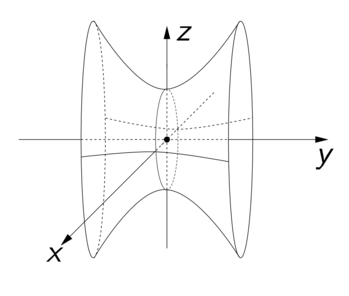
superficie.png (11.77 KiB) Exibido 5071 vezes

Observação

Se estiver interessado em assistir uma videoaula sobre o Hiperboloide de Uma Folha, eu gostaria de sugerir "43. Geometria Analítica - Equação do Hiperboloide". Esta videoaula está disponível em meu canal no YouTube, no endereço:

http://www.youtube.com/LCMAquino

[Danilo]

Muito obrigado Professor!!!!