 por Mayra Luna » Dom Jan 06, 2013 15:42
por Mayra Luna » Dom Jan 06, 2013 15:42
Olá, pessoal!
Estou com problemas para chegar ao resultado do seguinte exercício:
(Caderno de Exercícios - Anglo)
43. Considere os anagramas da palavra CAMARADA.
c) Quantos possuem as consoantes C, M, D e R juntas e nesta ordem? (Resposta: 5)
d) Quantos possuem as vogais juntas? (Resposta: 120)
Obrigada.
-
Mayra Luna
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Out 07, 2012 15:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Dom Jan 06, 2013 18:02
por DanielFerreira » Dom Jan 06, 2013 18:02
c)
CMDRAAAA
ACMDRAAA
AACMDRAA
AAACMDRA
AAAACMDR
d)
devemos considerar AAAA(quatro) como apenas A(um), veja:
CAAAAMDR = CAMDR
CMAAAADR = CMADR
Portanto, temos apenas 5 letras a permutar.
Daí,
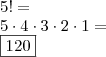
Espero ter ajudado!
Daniel Ferreira.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Mayra Luna » Dom Jan 06, 2013 19:20
por Mayra Luna » Dom Jan 06, 2013 19:20
Ah, eu pensei que tivesse que fazer conta na letra C.
Ajudou sim, muito obrigada!!
-
Mayra Luna
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Out 07, 2012 15:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Dom Jan 06, 2013 20:59
por DanielFerreira » Dom Jan 06, 2013 20:59
Segue outra forma de resolver a letra "c":
Consideremos CMDR como apenas uma letra, pois devem figurar juntas e nessa ordem (de acordo com o enunciado), daí:

Trata-se de uma permutação onde os elementos não são todos distintos.
Veja um exemplo:
Quantos anagramas possui a palavra VIVA?
resolução: 
Outro exemplo.
Quantos anagramas possui a palavra MATEMATICA?
resolução: 
Nota: o(s) número(s) que fica(m) em cima do

é a quantidade de vezes que uma mesma letra se repete, no caso de VIVA, 2 é a quantidade de V's; no segundo exemplo:
2 => quantidade de M's;
3 => quant. de A's;
2 => quant. de T's.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Mayra Luna » Dom Jan 06, 2013 23:37
por Mayra Luna » Dom Jan 06, 2013 23:37
Muitíssimo obrigada!
-
Mayra Luna
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Out 07, 2012 15:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Análise Combinatória
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


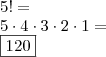




 é a quantidade de vezes que uma mesma letra se repete, no caso de VIVA, 2 é a quantidade de V's; no segundo exemplo:
é a quantidade de vezes que uma mesma letra se repete, no caso de VIVA, 2 é a quantidade de V's; no segundo exemplo: