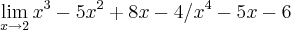


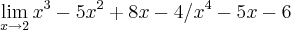

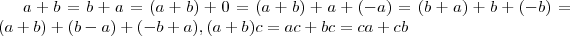 .
. 
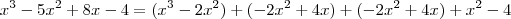
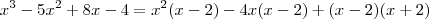
![x^3 -5x^2 + 8x - 4 = (x-2)[x^2 - 4x + x + 2] x^3 -5x^2 + 8x - 4 = (x-2)[x^2 - 4x + x + 2]](/latexrender/pictures/f5dab17557e2830a21abec2daac3f8ea.png)
 ou fazer o mesmo método acima .Deixo como exercício para você .
ou fazer o mesmo método acima .Deixo como exercício para você .  que aparecerá no númerador e no denominador . Note que isto só é possível pois
que aparecerá no númerador e no denominador . Note que isto só é possível pois 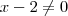 para
para 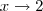 .
.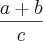


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.