a)
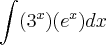
b)
![\int 15x^4/ \sqrt[]{1-x^10}dx \int 15x^4/ \sqrt[]{1-x^10}dx](/latexrender/pictures/60ef595aa823896d449e5ee9c7dde093.png) ( x elevado na 10)
( x elevado na 10)c)

na letra A , tentei chamar u=x, logo, du=dx... que com os ajustes, me resultou em :
 ... mas a resposta daria
... mas a resposta daria 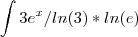 , porém a resposta correta é 3e^x/ln(3) + 1
, porém a resposta correta é 3e^x/ln(3) + 1na letra B, o x elevado na 10, eu separei em (x^2)*(x^2)*(x^2)*(x^2)*(x^2) e tirei da raíz ficando x^4 multiplicando a raiz de 1 - x^2... Aí cortei o x^4 que eu tirei da raiz com o x^4 que multiplica o 15 no numerador, enfim... a resposta que cheguei foi 15 arc sin(x) + c e no gabarito é: 3arc sin(X/5)
na letra C, eu realmente não sei começar essa , mas a respota correta é (6^2x)/2 + C
----------------------------------------------------
Desde já, muito obrigado


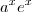 em integrais tente colocá-lo em uma unica base, no caso a base
em integrais tente colocá-lo em uma unica base, no caso a base  .
.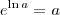 de forma que
de forma que  . Assim:
. Assim: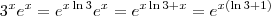 .
.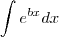 onde
onde  é uma constante e, no caso,
é uma constante e, no caso,  . Agora, faça
. Agora, faça  de forma que
de forma que 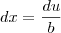 e então
e então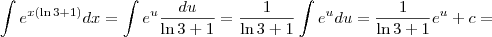



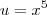 de onde
de onde 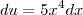 ... Assim o termo do numerador de
... Assim o termo do numerador de 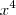 sumirá e o termo de
sumirá e o termo de 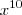 do binômio dentro da raiz poderá ser escrita como
do binômio dentro da raiz poderá ser escrita como  ... Agora basta continuar...
... Agora basta continuar... ... logo você terá
... logo você terá 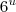 ... a integral de
... a integral de  ... Continue agora.
... Continue agora.
 .
.



