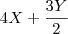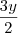por ViniRFB » Seg Dez 31, 2012 19:05
por ViniRFB » Seg Dez 31, 2012 19:05

=
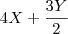
O procedimento a ser adotado é somar o X e o Y, mas nesse caso, do Y, deverá ser feito o MMC por isso
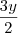
É isso amigos?
Excelente Final de Ano e um Feliz 2013 a todos.
Que sejamos felizes e saudáveis para alcançarmos nossas metas.
Grato
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielFerreira » Seg Dez 31, 2012 19:27
por DanielFerreira » Seg Dez 31, 2012 19:27
Olá
ViniRFB,
é isso aí!
Ou também:

Feliz 2013 para você também.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [UESC 2009 - Soma de Funções]
por Leocondeuba » Qui Jul 25, 2013 12:36
- 2 Respostas
- 2030 Exibições
- Última mensagem por Leocondeuba

Qui Jul 25, 2013 20:29
Funções
-
- Integral da soma/Soma das Integrais.
por Sobreira » Ter Abr 30, 2013 17:41
- 0 Respostas
- 2098 Exibições
- Última mensagem por Sobreira

Ter Abr 30, 2013 17:41
Cálculo: Limites, Derivadas e Integrais
-
- Funções reais. como resolver estas funções...
por LEANDRO HENRIQUE » Ter Mar 04, 2014 18:43
- 0 Respostas
- 3423 Exibições
- Última mensagem por LEANDRO HENRIQUE

Ter Mar 04, 2014 18:43
Funções
-
- Soma de PG
por a_guia » Seg Jan 04, 2010 22:19
- 1 Respostas
- 2026 Exibições
- Última mensagem por Molina

Seg Jan 04, 2010 22:54
Progressões
-
- Soma
por manuoliveira » Dom Mai 30, 2010 18:23
- 1 Respostas
- 8384 Exibições
- Última mensagem por Douglasm

Dom Mai 30, 2010 20:08
Binômio de Newton
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 =
= 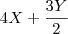
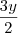

 =
=