a) Seja
 uma matriz
uma matriz  . Se
. Se 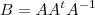 então
então  .
. Este exercício é simples ,mas estou em conflito com o mesmo . Na matemática
 significa matriz inversa da matriz
significa matriz inversa da matriz  . Mas ,devo considerar
. Mas ,devo considerar  como a matriz inversa da
como a matriz inversa da  ? Ou devo considerar a hipótese de
? Ou devo considerar a hipótese de  não existir ? Geralmente quando estamos buscando a inversa de uma matriz , por exemplo dada a matriz
não existir ? Geralmente quando estamos buscando a inversa de uma matriz , por exemplo dada a matriz 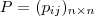 e a matriz
e a matriz 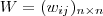 .Se
.Se 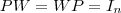 ,temos que
,temos que  isto é ,
isto é , é a matriz inversa da
é a matriz inversa da  .
. Afinal de contas , pelo enunciado única informação que sabemos é que
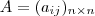 e logo após ele explícita
e logo após ele explícita  em função de
em função de  . O que quero dizer é que, dada uma matriz
. O que quero dizer é que, dada uma matriz 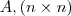 isto não significa que
isto não significa que  é invertível ,pois nem todas matriz quadradas são invertíveis .
é invertível ,pois nem todas matriz quadradas são invertíveis .Diante deste pensamento , eu concluir que esta informação é falsa . Pois ,
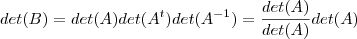 .
. Se
 é invertível , então
é invertível , então  logo
logo  . Mas isto contradiz ,meu pensamento .
. Mas isto contradiz ,meu pensamento .Em resumo :
Estou em conflito em considerar
 como a inversa da matriz
como a inversa da matriz  ou não . Pois no enunciado ele não diz que
ou não . Pois no enunciado ele não diz que  é invertível .
é invertível .Qual a opinião de vc's ?
Grato !


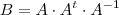 , isto automaticamente implica que
, isto automaticamente implica que  uma função dos reais nos reais. Se
uma função dos reais nos reais. Se 

 então
então  . Neste contexto meu pensamento acima justifica isto , certo ? Pois aqui não temos a certeza da existência da matriz inversa de
. Neste contexto meu pensamento acima justifica isto , certo ? Pois aqui não temos a certeza da existência da matriz inversa de 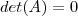 .Isto é definição .
.Isto é definição . em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.