Grandezas Matemáticas e Físicas

[Jhenrique]

Saudações caros!

O livro Os Fundamentos da Física - Volume 1 de Ramalho, Nicolau e Toledo, na pag. 225, quando explica o coeficiente de atrito diz que ele é uma grandeza adimensional e em seguida define o que é uma grandeza adimensional:

"Em Física, grandezas que não tem unidades são chamadas grandezas adimensionais."

Mas em [01. Geometria Analítica - Definição de Vetor][http://www.youtube.com/watch?v=oxUbiTdpWy8] Luiz Aquino afirma que vetor é uma grandeza e é representado convenientemente por meio de um segmento de reta orientado e que, portanto, é uma grandeza unidimensional.

Mas no curso de Geometria Analítica do Luiz Aquino*, ele trabalha com vetores sem trabalhar com unidades (a não ser que 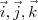, sejam unidades matemáticas, sei lá, é uma outra dúvida minha)... então quer dizer que os vetores são grandezas unidimensionais e adimensionais!? Não, obviamente,ou é um ou é outro! Estou bem confuso, a Matemática e a Física devem ser amigas... gostaria de maiores esclarecimentos!

*http://www.youtube.com/playlist?list=PLB7242F99B0310710

Obg!

[MarceloFantini]

O que é dimensão?

[Jhenrique]

Penso que dimensão é um conceito primitivo. Mas tentando definir isso, de modo geral, é um elemento que não pertence ao conjunto das ideias e sim ao do real.

[MarceloFantini]

A resposta é que um vetor é ambos. Na física, as 'dimensões' são as unidades. Em matemática, a dimensão pode ser várias coisas. No caso, como estamos em , a dimensão é um conceito de álgebra linear e assim dizemos que um vetor é um subespaço com dimensão 1, isto é, gerado por um único vetor.