 por ricardosanto » Sáb Dez 15, 2012 11:44
por ricardosanto » Sáb Dez 15, 2012 11:44
Determine o valor de M para que o plano pi = mx-4y-z+7=0 e a reta r: x=-1+p y=2+mp z= -2+3p. Sejam paralelos
vou mostrar o que eu entendo:
de um plano, tiramos o veto n : (m, -4,-1) que é perpendicular ao plano,
e da reta tiramos o vetor v; (1,m,3)
daí vi uma resolução que o cara fez n escalar v e ficou (m, -4m, -3) =0 (e igualou a zero) ficando -3m=3 m=-1
sei que o vetor v deve ser perpendicular ao plano.
aí eu n entendi, pq quando ele faz o produto escalar, e ele da 0
não entendi tbm o porque q ele usou apenas o vetor
-
ricardosanto
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Seg Abr 16, 2012 12:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia civil
- Andamento: cursando
 por young_jedi » Sáb Dez 15, 2012 20:26
por young_jedi » Sáb Dez 15, 2012 20:26
o porduto escalar de dois vetores perpendiculares é igual a zero
podemos ver isso atraves da equação
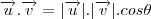
sendo

o angulo entre os dois vetores, se eles forem perpendiculares então o angulo sera 90º com isso o resultado do produto escalar é igual a 0 pois cosseno de 90 é igual a 0
voce tendo o vetor perpendicular ao plano, este vetor tem que ser perpendicualr tambem ao vetor diretor da reta
por isso ele faz o produto vetorial dos vetores e iguala a 0
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Retas paralelas a um mesmo plano
por ViniciusAlmeida » Qui Ago 27, 2015 19:52
- 0 Respostas
- 1254 Exibições
- Última mensagem por ViniciusAlmeida

Qui Ago 27, 2015 19:52
Geometria Analítica
-
- Retas Paralelas
por Cleyson007 » Seg Mai 25, 2009 08:34
- 3 Respostas
- 4275 Exibições
- Última mensagem por Marcampucio

Seg Mai 25, 2009 19:53
Trigonometria
-
- retas paralelas
 por Ana Maria da Silva » Ter Jun 18, 2013 11:37
por Ana Maria da Silva » Ter Jun 18, 2013 11:37
- 0 Respostas
- 1169 Exibições
- Última mensagem por Ana Maria da Silva

Ter Jun 18, 2013 11:37
Geometria Plana
-
- Retas paralelas
por outro » Qua Fev 15, 2017 11:59
- 2 Respostas
- 2596 Exibições
- Última mensagem por outro

Ter Fev 21, 2017 17:30
Geometria Plana
-
- Retas Paralelas - Ajuda
por bira19 » Dom Fev 19, 2012 16:21
- 1 Respostas
- 1441 Exibições
- Última mensagem por fraol

Dom Fev 19, 2012 21:59
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


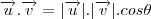
 o angulo entre os dois vetores, se eles forem perpendiculares então o angulo sera 90º com isso o resultado do produto escalar é igual a 0 pois cosseno de 90 é igual a 0
o angulo entre os dois vetores, se eles forem perpendiculares então o angulo sera 90º com isso o resultado do produto escalar é igual a 0 pois cosseno de 90 é igual a 0


 , avisa que eu resolvo.
, avisa que eu resolvo.

