 por joaofonseca » Qui Dez 13, 2012 17:25
por joaofonseca » Qui Dez 13, 2012 17:25
Seja uma equação diofantina linear de duas variáveis
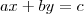
como poderei resolver recorrendo a matrizes?
Alguém já ouvio falar sobre este metedo de resolução?
Obrigado.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Cleyson007 » Qui Dez 13, 2012 17:45
por Cleyson007 » Qui Dez 13, 2012 17:45
Bom, a aquação acima tem solução se, e somente se, d dividir c.
Além disso, se x
o e y
o são tais que ax
o + by
o = c, então a solução geral da equação é dada por:

Não sei se é bem isso de que você está precisando..
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por joaofonseca » Sex Dez 14, 2012 11:51
por joaofonseca » Sex Dez 14, 2012 11:51
Essa é a solução paramétrica de uma equação diofantina, em que

e

são uma das soluções particulares. O sistema paramétrico dá todas as soluções da equação substituindo
k por um número inteiro.
O objetivo do meu estudo é encontrar um método de resolução mais intuitivo/algébrico, que parta de conceitos mais fundamentais, como por exemplo que uma equação diofantina é uma equação da reta no plano( onde só interessa as coordenadas com ambas as componentes inteiras).
Obrigado pela atenção
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Teoria dos Números
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação de Matrizes - Como Resolver
por juniocs » Qua Set 19, 2012 09:44
- 11 Respostas
- 6504 Exibições
- Última mensagem por Cleyson007

Qua Set 19, 2012 17:10
Álgebra Linear
-
- Como resolver matrizes
por zaza_mansano » Qua Out 19, 2011 12:36
- 2 Respostas
- 5179 Exibições
- Última mensagem por zaza_mansano

Qui Out 20, 2011 22:04
Matrizes e Determinantes
-
- matrizes COMO RESOLVER???
por LEANDRO HENRIQUE » Dom Mar 09, 2014 16:22
- 0 Respostas
- 1736 Exibições
- Última mensagem por LEANDRO HENRIQUE

Dom Mar 09, 2014 16:22
Matrizes e Determinantes
-
- como resolver essa multiplicaçao de matrizes
 por weverton » Sáb Jul 24, 2010 06:14
por weverton » Sáb Jul 24, 2010 06:14
- 2 Respostas
- 3458 Exibições
- Última mensagem por weverton

Dom Jul 25, 2010 23:02
Matrizes e Determinantes
-
- Equaçao diofantina
por silvia fillet » Sáb Nov 19, 2011 10:33
- 49 Respostas
- 40267 Exibições
- Última mensagem por vitorullmann

Qui Fev 14, 2013 18:18
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
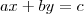 como poderei resolver recorrendo a matrizes?
como poderei resolver recorrendo a matrizes?
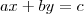 como poderei resolver recorrendo a matrizes?
como poderei resolver recorrendo a matrizes?


 e
e  são uma das soluções particulares. O sistema paramétrico dá todas as soluções da equação substituindo k por um número inteiro.
são uma das soluções particulares. O sistema paramétrico dá todas as soluções da equação substituindo k por um número inteiro.


 , avisa que eu resolvo.
, avisa que eu resolvo.

