 por Fabio Wanderley » Dom Dez 09, 2012 20:07
por Fabio Wanderley » Dom Dez 09, 2012 20:07
Boa noite a todos,
Alguém pode mostrar uma forma prática para se afirmar se uma dada função é limitada ou não?
Por exemplo, a função
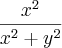
é limitada. Eu percebo isso intuitivamente. Mas gostaria de aprender uma forma de demonstrar formalmente.
Outro exemplo é a função

. Esta não é limitada (vi em um livro). Porém nem intuitivamente consigo notar isso. Assim, gostaria de aprender uma técnica ou demonstração formal a fim de apontar se uma dada função é limitada ou não.
Desde já agradeço!
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por e8group » Dom Dez 09, 2012 22:29
por e8group » Dom Dez 09, 2012 22:29
Para verificar se a função é limitada ,devemos observar se existe uma cosntante (número) pertencente ao domínio da função tal que o valor absoluto da sua imagem é menor ou igual a esta constante para quaisquer que seja os elementos pertencentes ao domínio da função . Ex.
A função

definida por
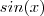
é limitada , pois
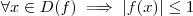
.Neste caso
![Im(f) \in [-1
,1] \forall x \in \mathbb{R} Im(f) \in [-1
,1] \forall x \in \mathbb{R}](/latexrender/pictures/0e5691591058dca91edacd03190e1fa7.png)
. Faça uma analogia com funções duas variáveis .
Vamos mostra que

é uma função limitada .Primeiro note que ,

.Isto contradiz apenas quando
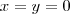
. Portanto se

vamos ter
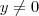
e vice-versa .
Para
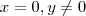
temos

e para
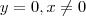
segue
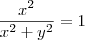
. Agora para

vamos ter que :

. Note que,

.Tome

e
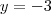
é fácil ver que
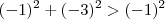
e assim sucessivamente .
Já

não podemos fazer a mesma afirmação .
Vale ressaltar que isto é apenas uma idéia intuitiva.Como estar a demonstração no livro ? Se tiver como , poderia postar aqui por favor ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Dom Dez 09, 2012 23:56
por MarceloFantini » Dom Dez 09, 2012 23:56
Dada uma função arbitrária não dá pra saber se ela é limitada ou não. Normalmente descobre-se isto tomando limites, calculando as derivadas, etc, mas não existe um método propriamente para detectar se a função é limitada ou não.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Fabio Wanderley » Seg Dez 10, 2012 10:53
por Fabio Wanderley » Seg Dez 10, 2012 10:53
Muito obrigado pela ajuda, santhiago e MarceloFantini!
santhiago escreveu:Como estar a demonstração no livro ? Se tiver como , poderia postar aqui por favor ?
santhiago, o autor não faz a demonstração. Ele só coloca para as duas funções um "note que".
Saudações!
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- como reconhecer uma função
por Erick Gabriel » Qui Abr 02, 2015 14:11
- 0 Respostas
- 1438 Exibições
- Última mensagem por Erick Gabriel

Qui Abr 02, 2015 14:11
Funções
-
- Como reconhecer se um número é primo?
por Kelvin Brayan » Dom Abr 24, 2011 15:16
- 2 Respostas
- 3544 Exibições
- Última mensagem por Kelvin Brayan

Dom Abr 24, 2011 16:28
Álgebra Elementar
-
- Como encontrar a área limitada por duas funções?
 por VenomForm » Qua Fev 27, 2013 15:09
por VenomForm » Qua Fev 27, 2013 15:09
- 2 Respostas
- 2886 Exibições
- Última mensagem por Russman

Qua Fev 27, 2013 19:14
Cálculo: Limites, Derivadas e Integrais
-
- FUNÇÃO LIMITADA
por jonas556440 » Ter Nov 11, 2014 10:27
- 1 Respostas
- 3144 Exibições
- Última mensagem por adauto martins

Ter Nov 11, 2014 20:11
Cálculo: Limites, Derivadas e Integrais
-
- Função Limitada
por Mateusus » Ter Abr 21, 2015 09:18
- 1 Respostas
- 2681 Exibições
- Última mensagem por adauto martins

Qua Abr 22, 2015 20:54
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
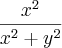 é limitada. Eu percebo isso intuitivamente. Mas gostaria de aprender uma forma de demonstrar formalmente.
é limitada. Eu percebo isso intuitivamente. Mas gostaria de aprender uma forma de demonstrar formalmente. . Esta não é limitada (vi em um livro). Porém nem intuitivamente consigo notar isso. Assim, gostaria de aprender uma técnica ou demonstração formal a fim de apontar se uma dada função é limitada ou não.
. Esta não é limitada (vi em um livro). Porém nem intuitivamente consigo notar isso. Assim, gostaria de aprender uma técnica ou demonstração formal a fim de apontar se uma dada função é limitada ou não.

 definida por
definida por 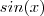 é limitada , pois
é limitada , pois 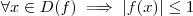 .Neste caso
.Neste caso ![Im(f) \in [-1
,1] \forall x \in \mathbb{R} Im(f) \in [-1
,1] \forall x \in \mathbb{R}](/latexrender/pictures/0e5691591058dca91edacd03190e1fa7.png) . Faça uma analogia com funções duas variáveis .
. Faça uma analogia com funções duas variáveis .  é uma função limitada .Primeiro note que ,
é uma função limitada .Primeiro note que ,  .Isto contradiz apenas quando
.Isto contradiz apenas quando 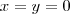 . Portanto se
. Portanto se  vamos ter
vamos ter 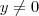 e vice-versa .
e vice-versa . 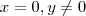 temos
temos  e para
e para 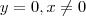 segue
segue 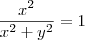 . Agora para
. Agora para  vamos ter que :
vamos ter que :  . Note que,
. Note que,  .Tome
.Tome  e
e 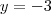 é fácil ver que
é fácil ver que 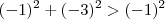 e assim sucessivamente .
e assim sucessivamente .  não podemos fazer a mesma afirmação .
não podemos fazer a mesma afirmação . 



 .
.



