 por pires_ » Dom Dez 09, 2012 20:35
por pires_ » Dom Dez 09, 2012 20:35
Uma janela tem a forma dum rectângulo encimado por um semicírculo com o diâmetro igual à base do rectangulo . A parte rectangular é de vidro transparente e a parte circular de vidro de cor que admite por m^2 metade da luz do vidro transparente . O perimetro total da janela é "P" . Determine , em função de "P" , as dimensões da janela que deixará entrar mais luz.
-
pires_
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Dom Dez 09, 2012 16:17
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: ciências e tecnologia
- Andamento: cursando
 por young_jedi » Seg Dez 10, 2012 10:35
por young_jedi » Seg Dez 10, 2012 10:35
um lado do retangulo mede x sendo este a base e tabem o diametro do semi-circulo, o outro ladó mede y
sendo assim a soma dos lados do retangulo com o semi-circulo sera dada pelo perimetro p
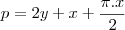
da onde tiramos
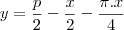
agora calculando as areas do retangulo e do semi-circulo


e a do semi-circulo
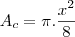
vamos admitir que no semi-circrulo a quantidade de luz permitida seja q e no retangulo seja 2q, então a quantidade de luz total sera
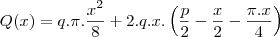

para encontrar seu valor de maximo derivamos com relação a x e igualamos a zero
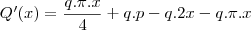
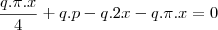
como tudo esta multiplicado por q podemos simplificar



este é o valor de x agora voce tem que encontra y
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por pires_ » Seg Dez 10, 2012 12:10
por pires_ » Seg Dez 10, 2012 12:10
como encontro o y ?
-
pires_
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Dom Dez 09, 2012 16:17
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: ciências e tecnologia
- Andamento: cursando
 por young_jedi » Seg Dez 10, 2012 12:58
por young_jedi » Seg Dez 10, 2012 12:58
nas primeiras equações quando relaciona o perimietro com x e y, substitua o valor de x encontrado e ache y, lembr-se de que tanto x como y vão ficar em função de p.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo]Alguém me ajuda nessa questão de calculo pfv.
por moeni » Seg Abr 04, 2022 21:54
- 0 Respostas
- 6487 Exibições
- Última mensagem por moeni

Seg Abr 04, 2022 21:54
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] calculo de integral - coordenada esferica
por fatalshootxd » Ter Mar 31, 2015 00:43
- 1 Respostas
- 4525 Exibições
- Última mensagem por adauto martins

Sáb Abr 04, 2015 16:13
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Cálculo Polinômio Interpolador
 por barbara-rabello » Qui Out 22, 2015 20:07
por barbara-rabello » Qui Out 22, 2015 20:07
- 1 Respostas
- 2653 Exibições
- Última mensagem por adauto martins

Sáb Out 24, 2015 11:00
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo] Exercícios de Calculo
por Thomas » Seg Mai 16, 2016 16:39
- 0 Respostas
- 0 Exibições
- Última mensagem por Visitante

Qua Dez 31, 1969 22:00
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo: Limites, Derivadas e Integrais] Cálculo de limites
por jeferson lopes » Ter Mar 26, 2013 08:49
- 2 Respostas
- 5559 Exibições
- Última mensagem por jeferson lopes

Ter Mar 26, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



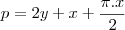
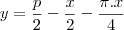


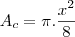
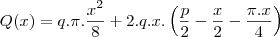

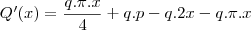
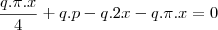






 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.