manuel_pato1 escreveu:Encontrar uma equação da parábola e suas interseções com os eixos coordenados, sendo dados:
a) F(0,0) eixo y=0 e passa por A(3,4)
(...)
Então , não entendi muito bem o que fazer nesse exercício.
como o eixo é y= 0 , a parábola é do tipo, y² = 2px , correto?
Pense um pouco: se o foco é em (0, 0), então o vértice não pode ser em (0, 0). Sendo assim, como pode a equação ser esta que você escreveu, na qual o vértice seria em (0, 0)?
Na verdade, como o eixo é y = 0 e o vértice não está em (0, 0), então ele está em
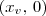
, com
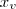
um número diferente de zero. Sendo assim, a equação será do tipo
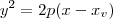
ou
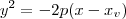
(dependendo da concavidade da parábola).
Precisamos então descobrir o valor de p e de
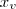
.
No exercício foram fornecidos o foco F = (0, 0) e o ponto A = (3, 4). Por outro lado, sabemos que qualquer ponto de uma parábola é tal que sua distância até o foco é igual a sua distância até a reta diretriz.
Calculando a distância de A até F, obtemos:
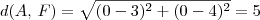
Sendo assim, a distância de A até a reta diretriz deve ser 5. Lembrando que o eixo é y = 0, temos que a reta diretriz será do tipo x = k (ou ainda, x - k = 0). Desse modo, temos que:
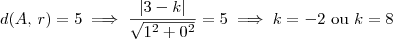
Podemos ter então duas possibilidades para a reta diretriz: (i) x = -2; (ii) x = 8. (Note que isso significa que na verdade o exercício terá duas respostas corretas.)
Possibilidade (i)Considerando que a reta diretriz seja x = -2, temos que a distância do foco F = (0, 0) até essa reta será 2. Sendo assim, teremos que p = 2. Disso concluímos que o vértice será V=(-1, 0). Além disso, teremos que a concavidade da parábola está voltada para a direita.
Portanto, a equação da parábola será dada por:
![y^2 = 2\cdot 2\cdot [x - (-1)]\implies y^2 - 4x - 4 = 0 y^2 = 2\cdot 2\cdot [x - (-1)]\implies y^2 - 4x - 4 = 0](/latexrender/pictures/60573e0f290abd0bdd3c8a442e4e4905.png)
Para determinar a interseção dessa parábola com o eixo x, basta substituir y = 0 na sua equação. Obtemos então o ponto (-1, 0).
Já para determinar a interseção dessa parábola com o eixo y, basta substituir x = 0 na sua equação. Obtemos então os pontos (0, -2) e (0, 2).
Possibilidade (ii)Considerando que a reta diretriz seja x = 8, temos que a distância do foco F = (0, 0) até essa reta será 8. Sendo assim, teremos que p = 8. Disso concluímos que o vértice será V=(4, 0). Além disso, teremos que a concavidade da parábola está voltada para a esquerda.
Portanto, a equação da parábola será dada por:
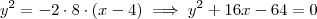
Para determinar a interseção dessa parábola com o eixo x, basta substituir y = 0 na sua equação. Obtemos então o ponto (4, 0).
Já para determinar a interseção dessa parábola com o eixo y, basta substituir x = 0 na sua equação. Obtemos então os pontos (0, -8) e (0, 8).
manuel_pato1 escreveu:b) F(0,-1) eixo x=0 e passa por A(4,2)
Tente resolver esse item considerando o procedimento utilizado para o item anterior. Note que nesse caso a equação da parábola será do tipo
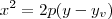
ou
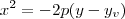
(dependendo da concavidade da parábola).


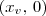 , com
, com 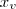 um número diferente de zero. Sendo assim, a equação será do tipo
um número diferente de zero. Sendo assim, a equação será do tipo 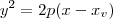 ou
ou 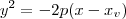 (dependendo da concavidade da parábola).
(dependendo da concavidade da parábola).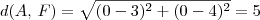
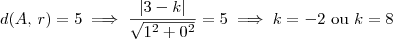
![y^2 = 2\cdot 2\cdot [x - (-1)]\implies y^2 - 4x - 4 = 0 y^2 = 2\cdot 2\cdot [x - (-1)]\implies y^2 - 4x - 4 = 0](/latexrender/pictures/60573e0f290abd0bdd3c8a442e4e4905.png)
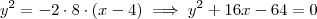
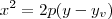 ou
ou 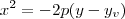 (dependendo da concavidade da parábola).
(dependendo da concavidade da parábola).
![\sqrt[2]{(k-3)^2 + (0-4)^2} \sqrt[2]{(k-3)^2 + (0-4)^2}](/latexrender/pictures/c8727dfa8c84a81c48b73ee34c13fc09.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.