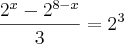 . Qual é a solução desta equação?
. Qual é a solução desta equação?Resp: 3 < x < 8
Tentei resolver assim:

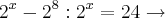
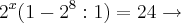
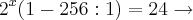

Mas não consigo chegar a resposta.
Onde estou errando? Está tudo errado?
Desde já agradeço a ajuda de todos
Abraços

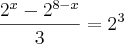 . Qual é a solução desta equação?
. Qual é a solução desta equação?
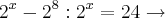
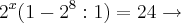
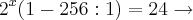


 . Note que
. Note que  , deste modo
, deste modo 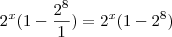 .Além disso ,observe que
.Além disso ,observe que 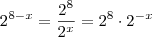 .
. 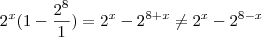 .Tome cuidado em assumir que
.Tome cuidado em assumir que 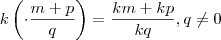 .Isto não é verdade .
.Isto não é verdade . 



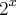 não alteraremos a igualdade . E , utilizando as propriedades
não alteraremos a igualdade . E , utilizando as propriedades  e
e 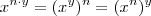 .Vamos obter ,
.Vamos obter , 
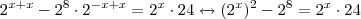
 em ambos lados , vamos ter
em ambos lados , vamos ter ![(2^x)^2 -2^8 = 2^x\cdot 24 \leftrightarrow [ (2^x)^2 -2^8]+(-2^x\cdot 24) = 2^x\cdot 24 - 2^x\cdot 24 \leftrightarrow (2^x)^2 -2^x\cdot 24 -2^8 = 0 (2^x)^2 -2^8 = 2^x\cdot 24 \leftrightarrow [ (2^x)^2 -2^8]+(-2^x\cdot 24) = 2^x\cdot 24 - 2^x\cdot 24 \leftrightarrow (2^x)^2 -2^x\cdot 24 -2^8 = 0](/latexrender/pictures/3b2d55db9be25ac3bb6ff0162dd61d99.png)
 . Como
. Como 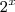 é estritamente positivo para quaisquer valores reais que
é estritamente positivo para quaisquer valores reais que  assumir (verifique ! ) vamos ter que ,
assumir (verifique ! ) vamos ter que , 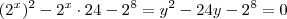 se e somente se
se e somente se 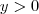 . Uma vez que temos solução para
. Uma vez que temos solução para  teremos para
teremos para  .
.  .
.  .
.

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.