 por karen » Qui Nov 29, 2012 10:01
por karen » Qui Nov 29, 2012 10:01
O número de pontos comuns aos gráficos das funções
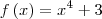
e
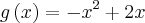
é:
Eu igualei as duas equações e cheguei a
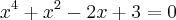
Eu tenho que achar as raízes e estas serão o números de pontos que se cruzam?
E como eu acho as raízes?
-
karen
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Mai 03, 2012 20:49
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Eletrônica
- Andamento: formado
 por young_jedi » Qui Nov 29, 2012 16:29
por young_jedi » Qui Nov 29, 2012 16:29
a melhor maneira que eu acho de resolver este exercicio é analisar as funções
analisando a função g(x)
percebemos que g(x) é uma parabola voltada para baixo suas raizes são 0 e 2 e seu vertice esta em x=1
sendo que
g(1)=1
portanto este é o maior valor possivel para g(x)
e analisando a função f(x) vemos que seu menor valor ocorre quando x=0
sendo que
f(0)=3
portanto este é o menor valor que assume a função f(x)
como 1<3 então chegamos a conclusão de que estas duas funções não se interceptam.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Fuvest-SP
por luanxd » Dom Fev 07, 2010 20:16
- 4 Respostas
- 5419 Exibições
- Última mensagem por luanxd

Ter Fev 09, 2010 11:06
Sistemas de Equações
-
- Fuvest
por CaAtr » Sex Abr 02, 2010 16:39
- 5 Respostas
- 4649 Exibições
- Última mensagem por Molina

Dom Abr 04, 2010 14:27
Sistemas de Equações
-
- LOG FUVEST
por PHANIE » Ter Abr 12, 2011 13:22
- 1 Respostas
- 14741 Exibições
- Última mensagem por Molina

Ter Abr 12, 2011 15:13
Logaritmos
-
- FUVEST 1
 por PHANIE » Ter Abr 26, 2011 15:53
por PHANIE » Ter Abr 26, 2011 15:53
- 3 Respostas
- 14138 Exibições
- Última mensagem por FilipeCaceres

Qua Mai 04, 2011 12:17
Geometria Plana
-
- fuvest 2
por PHANIE » Ter Abr 26, 2011 15:57
- 3 Respostas
- 5027 Exibições
- Última mensagem por FilipeCaceres

Qua Mai 04, 2011 12:33
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
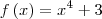 e
e 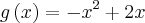 é:
é: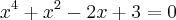

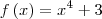 e
e 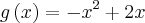 é:
é: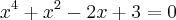


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.