 por Sobreira » Ter Nov 27, 2012 16:38
por Sobreira » Ter Nov 27, 2012 16:38
Quando eu tenho uma função deste tipo:
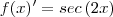
Eu sei que o resultado é este:
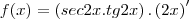
Agora quando eu tenho:

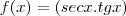
Eu gostaria de saber se eu estou calculando (de forma implícita o valor de
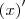
que vai dar 1, ou seja,
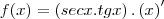
) ou simplesmente não estou calculando o valor da derivada de x e obtendo direto o resultado.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Ter Nov 27, 2012 19:36
por MarceloFantini » Ter Nov 27, 2012 19:36
Você está obtendo direto o resultado da derivada. Eu já pensei nisso, e a conclusão é que se pensarmos que estamos derivando implicitamente

este raciocínio não pára, de tal forma que toda derivada seria zero, pois você derivaria uma constante sempre no final.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sobreira » Ter Nov 27, 2012 22:25
por Sobreira » Ter Nov 27, 2012 22:25
Uma outra coisa que eu pensei também é o seguinte (não sei se está correto) no primeiro caso eu tenho uma função composta e então eu aplico a regra da cadeia:
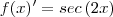
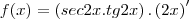
Já no segundo caso como eu tenho uma função "simples":

Não sei se posso aplicar a regra da cadeia também!!
O que acha??
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Ter Nov 27, 2012 22:27
por MarceloFantini » Ter Nov 27, 2012 22:27
Sim, você está correto: aplicamos a regra da cadeia apenas em funções compostas. A segunda função é elementar, portanto você já conhece sua derivada. Não existe regra da cadeia.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10878 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- Demonstração- secante
 por mathsoliver » Seg Abr 13, 2015 12:32
por mathsoliver » Seg Abr 13, 2015 12:32
- 1 Respostas
- 1754 Exibições
- Última mensagem por Cleyson007

Seg Abr 13, 2015 16:51
Equações
-
- seno e secante negativa
por Apotema » Seg Nov 23, 2009 14:36
- 2 Respostas
- 1983 Exibições
- Última mensagem por Apotema

Qua Nov 25, 2009 16:54
Trigonometria
-
- Função Secante e Cossecante
por gustavoluiss » Qui Jul 14, 2011 20:42
- 11 Respostas
- 5504 Exibições
- Última mensagem por gustavoluiss

Sáb Jul 16, 2011 15:19
Trigonometria
-
- [Cálculo] Integral da secante
por ARCS » Ter Ago 23, 2011 18:15
- 2 Respostas
- 8142 Exibições
- Última mensagem por LuizAquino

Ter Ago 23, 2011 23:02
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
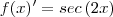
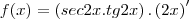

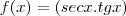
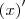 que vai dar 1, ou seja,
que vai dar 1, ou seja, 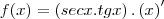 ) ou simplesmente não estou calculando o valor da derivada de x e obtendo direto o resultado.
) ou simplesmente não estou calculando o valor da derivada de x e obtendo direto o resultado.
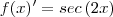
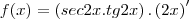

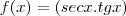
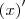 que vai dar 1, ou seja,
que vai dar 1, ou seja, 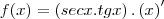 ) ou simplesmente não estou calculando o valor da derivada de x e obtendo direto o resultado.
) ou simplesmente não estou calculando o valor da derivada de x e obtendo direto o resultado.
 este raciocínio não pára, de tal forma que toda derivada seria zero, pois você derivaria uma constante sempre no final.
este raciocínio não pára, de tal forma que toda derivada seria zero, pois você derivaria uma constante sempre no final.

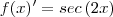
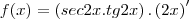






 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.