 , em que c é um número real positivo. Se o discriminante dessa equação é menor que zero, então
, em que c é um número real positivo. Se o discriminante dessa equação é menor que zero, então  é igual a:
é igual a:Primeiramente, eu sei que discriminante é o delta, portanto,
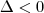 , então... as raízes são imaginárias.
, então... as raízes são imaginárias.Adotei a = x + yi e b = x -yi
De acordo com Girard, a x b = c/a,
(x+yi) (x-yi) = c²
x² + y² = c²
Não sei resolver a partir daí.






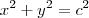



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)