 por SCHOOLGIRL+T » Qui Nov 15, 2012 17:44
por SCHOOLGIRL+T » Qui Nov 15, 2012 17:44
Em uma substância radioativa, o número N de átomos de um isótopo de um certo elemento é reduzido à metade após um período de 5000 anos. Ou seja, se t representa o tempo medido em unidades de 5000 anos, e No corresponde ao número de átomos desse isótopo no instante t=0, então

. Se a substância apresenta 100.000 átomos desse isótopo no instante t=o, então o número de anos necessários para que o número desses átomos seja igual a 100, admitindo
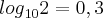
, é?
-
SCHOOLGIRL+T
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Nov 07, 2012 08:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Sex Nov 23, 2012 09:34
por e8group » Sex Nov 23, 2012 09:34

descresce ao passar do tempo , no instante

teremos

.
Após

unidades de tempo , temos que

. Qual valor que

deve assumir para termos

, sabendo que
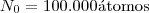
?
Basta resolver ,

. Aplicando logaritmo nos dois lados , vem que
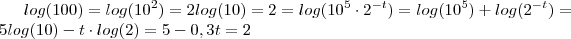
.
Somando - 5 dos dois lados e após isto mutiplicando ambos lados por
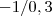
, segue que
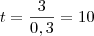
.
Como

é medido em unidades 5000 anos , concluímos que
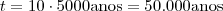
.
Comente qualquer dúvida .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por SCHOOLGIRL+T » Sex Nov 23, 2012 18:51
por SCHOOLGIRL+T » Sex Nov 23, 2012 18:51
santhiago escreveu:
descresce ao passar do tempo , no instante

teremos

.
Após

unidades de tempo , temos que

. Qual valor que

deve assumir para termos

, sabendo que
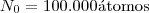
?
Basta resolver ,

. Aplicando logaritmo nos dois lados , vem que
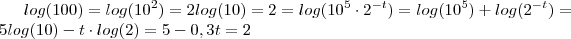
.
Somando - 5 dos dois lados e após isto mutiplicando ambos lados por
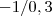
, segue que
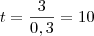
.
Como

é medido em unidades 5000 anos , concluímos que
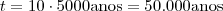
.
Comente qualquer dúvida .
Entendi direitinho. Obrigada.
-
SCHOOLGIRL+T
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Nov 07, 2012 08:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 . Se a substância apresenta 100.000 átomos desse isótopo no instante t=o, então o número de anos necessários para que o número desses átomos seja igual a 100, admitindo
. Se a substância apresenta 100.000 átomos desse isótopo no instante t=o, então o número de anos necessários para que o número desses átomos seja igual a 100, admitindo 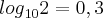 , é?
, é?
 . Se a substância apresenta 100.000 átomos desse isótopo no instante t=o, então o número de anos necessários para que o número desses átomos seja igual a 100, admitindo
. Se a substância apresenta 100.000 átomos desse isótopo no instante t=o, então o número de anos necessários para que o número desses átomos seja igual a 100, admitindo 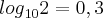 , é?
, é?
 descresce ao passar do tempo , no instante
descresce ao passar do tempo , no instante  teremos
teremos  .
.  unidades de tempo , temos que
unidades de tempo , temos que  . Qual valor que
. Qual valor que  deve assumir para termos
deve assumir para termos  , sabendo que
, sabendo que 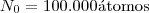 ?
?  . Aplicando logaritmo nos dois lados , vem que
. Aplicando logaritmo nos dois lados , vem que 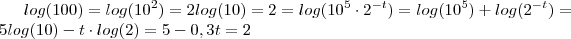 .
. 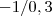 , segue que
, segue que 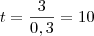 .
.  é medido em unidades 5000 anos , concluímos que
é medido em unidades 5000 anos , concluímos que 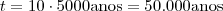 .
.
descresce ao passar do tempo , no instante
teremos
.
unidades de tempo , temos que
. Qual valor que
deve assumir para termos
, sabendo que
?
. Aplicando logaritmo nos dois lados , vem que
.
, segue que
.
é medido em unidades 5000 anos , concluímos que
.
