 por Sherminator » Sex Nov 23, 2012 16:31
por Sherminator » Sex Nov 23, 2012 16:31
Boa tarde pessoal, nem sei como resolver este problema, alguém me ajuda? Não consigo de forma alguma
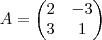

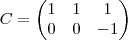
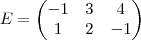
Sabendo que a matriz D=A*B, determinar a matriz X tal que:

(E+C) = O

A, B, C e E são matrizes reais.
Primeiro não consigo calcular a A*B devido a ter a fração
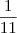
na matriz B
Segundo não tenho mesmo a mínima ideia de como se calcula o X, depois também não sei o que significa o O no final
Alguém me pode ajudar? Ou então resolver para eu ver como se faz?
-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
 por MarceloFantini » Sex Nov 23, 2012 23:29
por MarceloFantini » Sex Nov 23, 2012 23:29
Quando um número multiplica uma matriz significa que ele multiplica todos os elementos da matriz, portanto pode ser posto em evidência. Para efetuar o produto

faça como uma multiplicação normal de matrizes, e depois multiplique todos os elementos por
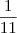
.
A notação
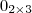
quer dizer a matriz nula com duas linhas e três colunas, ou
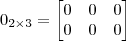
.
Para calcular a matriz

resolva normalmente:
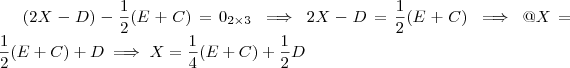
.
Agora é só calcular. A soma

é tranquilo, basta somar componente a componente. O que dá um pouco mais de trabalho é a matriz

. Depois é só multiplicar pelos respectivos coeficientes e terá completado a solução.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sherminator » Sáb Nov 24, 2012 07:40
por Sherminator » Sáb Nov 24, 2012 07:40
Então a matriz D ficaria assim?

Ou assim depois de multiplicada?
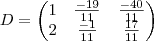
Como seria mais correto deixá-la?
Já reparei que depois é uma maneira de isolar o X, verdade?
Então já agora me explique como poderia eu calcular o X nestas aqui, visto agora ter mais de um X, não estou a ver forma de o isolar.
![\frac{1}{2} (X+A) = 3[X+(A-X)]+E \frac{1}{2} (X+A) = 3[X+(A-X)]+E](/latexrender/pictures/af125c81e8f4d6499ab763bb43afdfb4.png)
aqui tenho 3 X, como arranjo forma de os calcular?
Nesta parece ser mais difícil ainda:
![\frac{1}{3}(AE^T+X) = 2CI+\frac{1}{6}[X+(A-X)-A] \frac{1}{3}(AE^T+X) = 2CI+\frac{1}{6}[X+(A-X)-A]](/latexrender/pictures/999a0b1be12f14096953face00d1d3a6.png)
-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
 por MarceloFantini » Sáb Nov 24, 2012 17:12
por MarceloFantini » Sáb Nov 24, 2012 17:12
Acredito que não exista um modo melhor de deixá-la. Tecnicamente quanto mais simplificado melhor, então seria a segunda opção.
Sim, é verdade: a menos de "divisão" de matrizes, você trabalha com matrizes como números: multiplicação à esquerda ou direita, soma e subtração de matrizes e multiplicação por escalares (números).
Sobre a expressão
![\frac{1}{2}(X+A) = 3[X + (A-X)] +E \frac{1}{2}(X+A) = 3[X + (A-X)] +E](/latexrender/pictures/a39ab71f9fa41cf84d344c4d9317849c.png)
, note que

, logo ela torna-se
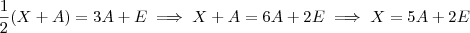
.
Na segunda expressão que mostrou, acredito que esteja errada. A multiplicação

não é possível pois

é uma matriz

, logo
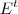
é uma matriz

. Como o número de linhas é diferente do número de colunas a multiplicação não é possível.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda a resolver
por Sherminator » Sáb Nov 24, 2012 20:04
- 5 Respostas
- 3666 Exibições
- Última mensagem por Sherminator

Dom Nov 25, 2012 10:33
Matrizes e Determinantes
-
- Ajuda pra resolver exercicio
 por Brunna013 » Ter Jun 03, 2008 11:22
por Brunna013 » Ter Jun 03, 2008 11:22
- 4 Respostas
- 42153 Exibições
- Última mensagem por Molina

Seg Mai 03, 2010 14:33
Trigonometria
-
- ALguem me ajuda a resolver?
por jujuba100054 » Qua Set 28, 2011 19:47
- 1 Respostas
- 1549 Exibições
- Última mensagem por Neperiano

Qui Set 29, 2011 16:25
Polinômios
-
- [Ajuda] RESOLVER Equação
por hudsontr » Seg Out 10, 2011 17:44
- 1 Respostas
- 4379 Exibições
- Última mensagem por Neperiano

Ter Out 11, 2011 15:19
Trigonometria
-
- Resolver função - Ajuda
por LAZAROTTI » Qua Mai 02, 2012 01:51
- 1 Respostas
- 1199 Exibições
- Última mensagem por Russman

Qua Mai 02, 2012 05:51
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
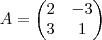

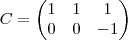
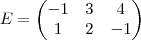
 (E+C) = O
(E+C) = O
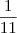 na matriz B
na matriz B

 faça como uma multiplicação normal de matrizes, e depois multiplique todos os elementos por
faça como uma multiplicação normal de matrizes, e depois multiplique todos os elementos por 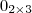 quer dizer a matriz nula com duas linhas e três colunas, ou
quer dizer a matriz nula com duas linhas e três colunas, ou 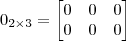 .
. resolva normalmente:
resolva normalmente: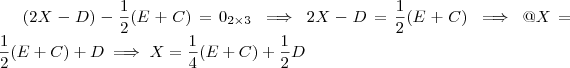 .
. é tranquilo, basta somar componente a componente. O que dá um pouco mais de trabalho é a matriz
é tranquilo, basta somar componente a componente. O que dá um pouco mais de trabalho é a matriz  . Depois é só multiplicar pelos respectivos coeficientes e terá completado a solução.
. Depois é só multiplicar pelos respectivos coeficientes e terá completado a solução.


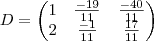
![\frac{1}{2} (X+A) = 3[X+(A-X)]+E \frac{1}{2} (X+A) = 3[X+(A-X)]+E](/latexrender/pictures/af125c81e8f4d6499ab763bb43afdfb4.png) aqui tenho 3 X, como arranjo forma de os calcular?
aqui tenho 3 X, como arranjo forma de os calcular?![\frac{1}{3}(AE^T+X) = 2CI+\frac{1}{6}[X+(A-X)-A] \frac{1}{3}(AE^T+X) = 2CI+\frac{1}{6}[X+(A-X)-A]](/latexrender/pictures/999a0b1be12f14096953face00d1d3a6.png)
![\frac{1}{2}(X+A) = 3[X + (A-X)] +E \frac{1}{2}(X+A) = 3[X + (A-X)] +E](/latexrender/pictures/a39ab71f9fa41cf84d344c4d9317849c.png) , note que
, note que  , logo ela torna-se
, logo ela torna-se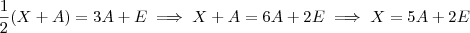 .
. não é possível pois
não é possível pois  é uma matriz
é uma matriz  , logo
, logo 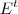 é uma matriz
é uma matriz  . Como o número de linhas é diferente do número de colunas a multiplicação não é possível.
. Como o número de linhas é diferente do número de colunas a multiplicação não é possível.