2) UMA PARTICULA MOVE-SE NO SENTIDO HORÁRIO SOBRE UM CÍRCULO DE CENTRO EM (1,1) E RAIO 2, COM VELOCIDADE ESCALAR CONSTANTE IGUAL A 6. DETERMINE UMA FUNÇÃO CUJA TRAJETÓRIA DESCREVE O MOVIMENTO DA PARTÍCULA.
minha tentativa:
parametrização de um círculo com centro em (0,0) e raio 1:
w(t) = (cost, sent)
parametrização de um círculo com centro em (0,0) e raio 2:
w(t) = (2cost, 2sent)
parametrização de um círculo com centro em (1,1) e raio 2:
w(t) = (1+2cost, 1+2sent)
parametrização de um círculo com centro em (1,1) e raio 2 e que descreva um movimento horário:
w(t) = (1+2sent,1+2cost)
e para mim seria essa a resposta..
mas eu nem utilizei o dado que foi dado, de que a velocidade escalar é constante e igual a 6.
sei que a derivada da trajetória é a velocidade instantânea, e que a norma dessa derivada, || v || é a velocidade escalar. mas como eu deveria ter usado esse dado? tá tudo errado ou o que? me ajudem, por favor

será que seria:
w(t) = (1+2sen(6t),1+2cos(6t))??
como vocês resolveriam ele? :p


 , assim teremos
, assim teremos 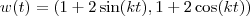 .
. , ou seja, no topo da circunferência. Isto não faz tanta diferença mas é interessante perceber.
, ou seja, no topo da circunferência. Isto não faz tanta diferença mas é interessante perceber.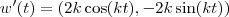 .
. ,
, . Existe uma resposta negativa para
. Existe uma resposta negativa para  , mas isto significaria reverter a orientação novamente, o que não queremos, portanto descartei-a.
, mas isto significaria reverter a orientação novamente, o que não queremos, portanto descartei-a. .
.

 foi que ao derivar poderíamos ter uma constante a mais multiplicando o seno e o cosseno de tal forma que a velocidade se alterasse.
foi que ao derivar poderíamos ter uma constante a mais multiplicando o seno e o cosseno de tal forma que a velocidade se alterasse.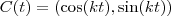 , temos que
, temos que  e assim
e assim 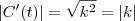 .
.

 , avisa que eu resolvo.
, avisa que eu resolvo.

