 por replay » Seg Nov 19, 2012 16:58
por replay » Seg Nov 19, 2012 16:58
Se

, com 1<=

<= 10, então

é igual a:
a)24
b)25
c)26
d)27
e)28
Eu estou em duvida como iniciar o exercicio, alguêm me da uma luz que eu termino ele aqui.
Acho que fazendo
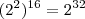
mas não sei oque simplificar no caso do
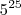
Edit:
Pensando aqui, o expoente

deve ser uma das alternativas e a base tem que ser de 1 ao 10 seria isso ?
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Seg Nov 19, 2012 23:13
por MarceloFantini » Seg Nov 19, 2012 23:13
Note que
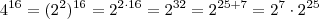
.
Voltando à equação original, temos

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por replay » Seg Nov 19, 2012 23:27
por replay » Seg Nov 19, 2012 23:27
Marcelo.
Deduzo daqui que para a equação ficar completa eu resolvo
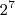
= 128
Como 128 não está entre 1 e 10 deduzo que preciso diminuir as casa decimais(é o unico modo de satisfazer a equação):
128 . 10^{25}
12,8 . 10^{26}
1,28 . 10^{27}
Sendo questão D como alternativa correta.
Seria isso ?
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Seg Nov 19, 2012 23:31
por MarceloFantini » Seg Nov 19, 2012 23:31
Sim, é isso.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por replay » Seg Nov 19, 2012 23:35
por replay » Seg Nov 19, 2012 23:35
Não entendo como você escreve na assinatura Futuro Matematico.
Pra min você ja é um grande matematico, queria ter um pouco desse esforço.
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Seg Nov 19, 2012 23:38
por MarceloFantini » Seg Nov 19, 2012 23:38
Essa assinatura já é bem antiga, eu coloquei na época que meu nome no fórum era apenas Fantini e as pessoas achavam que era mulher. Coloquei a assinatura numa tentativa de reduzir o número de enganos. Eventualmente pedi que trocassem meu nome de usuário e o problema resolveu-se, mas deixei a assinatura.
Além disso, estou longe de ser um grande matemático. Tem muito esforço, tempo, dedicação e habilidade necessários antes de chegar lá, mas agradeço pelo elogio.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Série de potÊncia] Expansão de séries de potência
 por Adonias 7 » Qua Jun 01, 2016 09:05
por Adonias 7 » Qua Jun 01, 2016 09:05
- 0 Respostas
- 3690 Exibições
- Última mensagem por Adonias 7

Qua Jun 01, 2016 09:05
Sequências
-
- Potência de potência... não sei ao certo se entendi...
por Vennom » Sáb Fev 20, 2010 10:42
- 3 Respostas
- 3776 Exibições
- Última mensagem por mottasky

Ter Out 04, 2011 02:03
Álgebra Elementar
-
- [Potencia] soma de potencia com letras
por carla villela » Qui Mar 01, 2012 21:04
- 8 Respostas
- 8623 Exibições
- Última mensagem por carla villela

Qui Mar 01, 2012 22:18
Sistemas de Equações
-
- Potenciação - Potência de potência
por Ana Paula MMS » Sáb Jan 11, 2014 14:59
- 1 Respostas
- 2635 Exibições
- Última mensagem por Cleyson007

Sáb Jan 11, 2014 17:27
Aritmética
-
- (Potencia) equação com potencia
por Thiago1986Iz » Dom Jul 24, 2016 12:53
- 1 Respostas
- 2043 Exibições
- Última mensagem por DanielFerreira

Dom Jul 24, 2016 16:00
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , com 1<=
, com 1<= <= 10, então
<= 10, então  é igual a:
é igual a: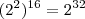 mas não sei oque simplificar no caso do
mas não sei oque simplificar no caso do 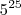
 deve ser uma das alternativas e a base tem que ser de 1 ao 10 seria isso ?
deve ser uma das alternativas e a base tem que ser de 1 ao 10 seria isso ?

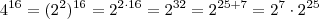 .
. .
.

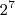 = 128
= 128
 .
.



