Gente tenho uma prova amanhã sobre probabilidade o professor passou estes exercicios para estudar e não consigo resolver... alguem pode me explicar como de uma forma bem simples? se possivel coloque as respostas para eu tentar conferir depois.
Você joga 5 moedas idênticas para alto todas ao mesmo tempo.
a) Qual a probabilidade dar 5 caras?
b) Qual a probabilidade de dar 2 caras?
c) Qual a probabilidade de dar pelo menos 3 caras?
d) Qual a probabilidade de dar no máximo 2 coroas?
Obrigado!







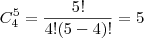



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.