 por manuel_pato1 » Sáb Nov 17, 2012 20:53
por manuel_pato1 » Sáb Nov 17, 2012 20:53
Opa, beleza galera?
estou com um exercício que está me complicando , mas acredito que ele não seja dos mais complicadoos para quem já tenha algum conhecimento de elipse.
Ele quer que eu obtenha a equação da elipse com os dados que ele dá:
a) eixo maior =10 , F1(2,-1) F2(2,5)
b)Vértices A1(0,6) ,A2(0,-6) e passando pelo ponto P(3,2)
c)F1(-1,3) , F2(-1,5) e excnetricidade = 2/3
----->Na letra a, o eixo maior sendo igual a 10, obtenho que a=5 , correto?
E dos dois focos tiro a relação de que 2c=6, logo o c=3
a²=b²+c²
25-9= b²
b=+/- 4
Centro( 2,2)
OBs: eu achei o Centro através do esboço prévio da elipse, não sei se tem algum processo algébrico para descobrir.
(x-2)²/16 + (y-2)²/25=1
25(x² + 4 -4x) + 16(y² + 4 -4y) = 1
25x² -100x +16y² -64y +(164-1) = 0
25x² -100x + 16y² - 64y + 163= 0
porém, o resultado dá: 25x² - 100x + 16y² - 64y - 236
De onde saiu esse 236 ?? fiquei totalmente perdido nessa parte.
-----> Na letra b
2a=12 , a=6
eu penso que como P pertence a elipse , eu faria:
9/a² + 4/36 = 1
só que achho que não é assim, pois chego que a² = raiz de 81/8
------> letra C tá dífícil de começar, pois só sei que 2c=4 , c=2
e da excentricidade eu não sei quanto é c, pois sei que ele é 2, mas na fórmula aparece c/a = 3/2
-
manuel_pato1
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Ter Set 18, 2012 22:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por young_jedi » Dom Nov 18, 2012 10:49
por young_jedi » Dom Nov 18, 2012 10:49
a)
voce chegou que

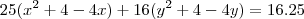


b)
2a=12 a=6

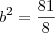
então a equação fica
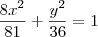
c)
2c=5-3
c=1
da excentricidade tiramos



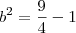
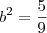
então a equação fica

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por manuel_pato1 » Qua Nov 21, 2012 19:47
por manuel_pato1 » Qua Nov 21, 2012 19:47
Brigadão meu velho.
Em relação a letra C, eu fiz de um jeito alternativo, mas não sei se está certo. Tu pode me dizer se está certa a minha resolução?
Como nos focos só se altera a ordenada , preservei a abcissa para descobrir o centro, e fiz a mediana do -3 ao 5 ( de cabeça)
daí ,descobri que o centro é (-1,1)
como sei que e=2/3 , e do foco tirei que 2c=8 -> c=4
se 4/a=2/3 -> a=6
a²= b² + c²
36-16=b²
b²=20
então
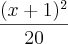
+

= 720
36(x + 1)² + 20(y-1)² = 720
36x² + 72x + 20y² - 40y - 664=0 (/4)
9x² + 18x + 5y² - 10y - 1666 = 0
o resultado bateu com o do livro, mas não sei se esse método é correto.
abraço
-
manuel_pato1
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Ter Set 18, 2012 22:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por young_jedi » Qua Nov 21, 2012 20:13
por young_jedi » Qua Nov 21, 2012 20:13
Amigo esta certo sim seu procedimento
eu tinha pensado que os focos eram f(-1,3) e f(-1,5) mais na verdade é f(-1,-3) e f(-1,5)
por isso minha resposta deu diferente da sua
mais a sua resposta e seu raciocinio estão corretos sim!!!
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por manuel_pato1 » Qua Nov 21, 2012 20:44
por manuel_pato1 » Qua Nov 21, 2012 20:44
Muito obrigado ,cara. Tu tem me ajudado muito nos exercícios mais complicados =D
-
manuel_pato1
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Ter Set 18, 2012 22:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (CÕNICAS) Elipse
por manuel_pato1 » Sex Nov 23, 2012 01:04
- 4 Respostas
- 2365 Exibições
- Última mensagem por manuel_pato1

Sex Nov 23, 2012 14:42
Geometria Analítica
-
- [Cônicas] Dúvida exerc. elipse
por MrJuniorFerr » Qua Out 31, 2012 12:58
- 1 Respostas
- 1530 Exibições
- Última mensagem por young_jedi

Qua Out 31, 2012 21:00
Geometria Analítica
-
- Cônicas - Elipse - Só uma dúvida simples
por samra » Sex Jan 24, 2014 01:39
- 2 Respostas
- 1687 Exibições
- Última mensagem por samra

Sex Jan 24, 2014 19:21
Geometria Analítica
-
- Cônicas: Elipse, me ajudem, por favor!
por felipe_08 » Qui Mai 28, 2015 22:48
- 0 Respostas
- 1201 Exibições
- Última mensagem por felipe_08

Qui Mai 28, 2015 22:48
Geometria Analítica
-
- cônicas:equação da parabola
por may » Ter Jul 12, 2011 21:35
- 2 Respostas
- 11430 Exibições
- Última mensagem por may

Sex Jul 15, 2011 00:46
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



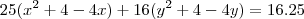



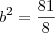
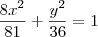



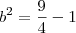
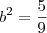


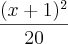 +
+  = 720
= 720




