![\int_{4}^{5}\sqrt[2]{x^2 - 16}/ x^2 \approx 0,09 \int_{4}^{5}\sqrt[2]{x^2 - 16}/ x^2 \approx 0,09](/latexrender/pictures/3b36ae9b4af2c44ee5cd7dff94ed6f7d.png)
aqui desenvolvi até
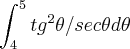
agora naõ sei continuar

![\int_{4}^{5}\sqrt[2]{x^2 - 16}/ x^2 \approx 0,09 \int_{4}^{5}\sqrt[2]{x^2 - 16}/ x^2 \approx 0,09](/latexrender/pictures/3b36ae9b4af2c44ee5cd7dff94ed6f7d.png)
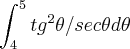

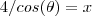 de onde
de onde 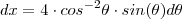 .
. 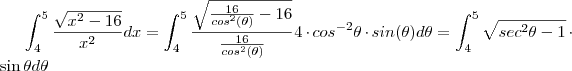
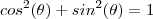 multiplicando ambos lados da igualdade por
multiplicando ambos lados da igualdade por 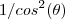 e logo após somando
e logo após somando  , vamos obter que ,
, vamos obter que , 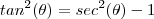 que nos leva ,
que nos leva , 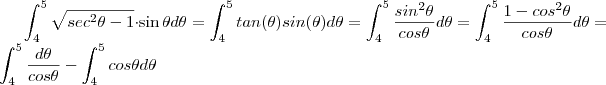

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)