 por joedsonazevedo » Qui Nov 15, 2012 11:34
por joedsonazevedo » Qui Nov 15, 2012 11:34
Geste estou tentado resolver a seguinte questão envolvendo polinômios...
e quer saber o intervalo...Socorro por favor! preciso aprender como se
resolve tais questões... e primeiramente.. interpretá-las.. pois minha maior
dificuldade... não são os cálculos mas interpretar a questão...
--> Considerando-se que o polinômio
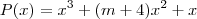
tem uma única raiz real, pode-se afirmar
que m pertence ao intervalo:
a) ]-8,-6[
b) ]-6,-2[
c) ]-2,-1[
d) ]2,6[
e) ]6,8[
_____________________________________Muito Obrigado...
-
joedsonazevedo
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qui Nov 08, 2012 14:23
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. em Informática
- Andamento: formado
 por DanielFerreira » Qui Nov 15, 2012 13:31
por DanielFerreira » Qui Nov 15, 2012 13:31
Joedson,
bom dia!
Para encontrar as raízes devemos fazer
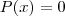
, veja:
![\\ x^3 + (m + 4)x^2 + x = 0 \\\\ x \left [ x^2 + (m + 4)x + 1 \right ] = 0 \\ x^3 + (m + 4)x^2 + x = 0 \\\\ x \left [ x^2 + (m + 4)x + 1 \right ] = 0](/latexrender/pictures/a050b94109cd95d5b827aeab21a98d98.png)
Da última equação (fatorada) temos:

ZERO é uma das raízes e é REAL, portanto, para encontrar as outras raízes (complexas) devemos fazer
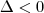
.
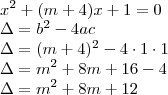
Já que sabemos o valor de

...
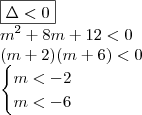
Resta-nos estudar os sinais!
Daí,

Alternativa "
b"
Comente qualquer dúvida!1
Daniel F.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [polinômios] questão uel
por Flavia R » Ter Ago 30, 2011 12:45
- 0 Respostas
- 1816 Exibições
- Última mensagem por Flavia R

Ter Ago 30, 2011 12:45
Polinômios
-
- Polinômios - Questão
por iceman » Dom Mai 27, 2012 18:23
- 1 Respostas
- 1556 Exibições
- Última mensagem por DanielFerreira

Dom Mai 27, 2012 18:26
Polinômios
-
- Polinômios - Questão
por iceman » Dom Mai 27, 2012 23:51
- 1 Respostas
- 1492 Exibições
- Última mensagem por Cleyson007

Ter Mai 29, 2012 17:39
Polinômios
-
- Questão do ITA-SP sobre Polinômios
por PedroCunha » Qui Nov 15, 2012 08:36
- 15 Respostas
- 15460 Exibições
- Última mensagem por PedroCunha

Ter Nov 20, 2012 21:31
Polinômios
-
- Questão de polinômios(UFMG-2007)
por Thiago Silveira » Dom Ago 15, 2010 18:07
- 4 Respostas
- 8169 Exibições
- Última mensagem por Thiago Silveira

Seg Ago 16, 2010 18:03
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
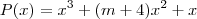


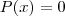 , veja:
, veja:![\\ x^3 + (m + 4)x^2 + x = 0 \\\\ x \left [ x^2 + (m + 4)x + 1 \right ] = 0 \\ x^3 + (m + 4)x^2 + x = 0 \\\\ x \left [ x^2 + (m + 4)x + 1 \right ] = 0](/latexrender/pictures/a050b94109cd95d5b827aeab21a98d98.png)

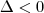 .
.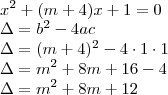
 ...
...




 , avisa que eu resolvo.
, avisa que eu resolvo.

