derivação de funções

por **SILMARAKNETSCH** » Sex Nov 09, 2012 16:17

obs só sei colocar exponente 2 e 3 mas abaixo preciso derivadas com exponentes 4 então vou colocar 4 após o x que é o exponente 4

a) f(x) = x4 - 5x³ + 3x - 2

b) f(x) = x² - 2) . (2x+3)

por **SILMARAKNETSCH** » Sex Nov 09, 2012 16:18

tenho que calcular as derivadas dessas funções

por **DanielFerreira** » Dom Nov 11, 2012 13:46

Silmaraknetsch,
para postar as equações faça assim:

digite a equação: f(x) = x^4 - 5x^3 + 3x - 2

coloque-a entre [t e x] [/t e x]

escreve-se tex junto, coloquei separado apenas para que pudesse visualizar.

Ficará

Quanto a quantidade de questões por tópico, é permita apenas uma. Abra um tópico para cada dúvida/questão.
Inclusive, é interessante você expor a forma como tentou resolver a questão.

Segue a resolução do item a):

$\\ f(x) = x^4 - 5x^3 + 3x - 2 \\\\ f(x) = x^4 - 5x^3 + 3x^1 - 2x^0 \\\\ f'(x) = 4 \cdot (x)^{4 - 1} - 5 \cdot 3 \cdot (x)^{3 - 1} + 3 \cdot 1 \cdot (x)^{1 - 1} \cancel{- 2 \cdot 0 \cdot (x)^{0 - 1}} \\\\ f'(x) = 4x^3 - 15x^2 + 3x^0 - 0 \\\\ \boxed{f'(x) = 4x^3 - 15x^2 + 3}$

Nota: o termo que ficou ilegível é: $\,\, \mathbf{- 2 \cdot 0 \cdot (x)^{0 - 1}}$

Espero ter ajudado!

por **SILMARAKNETSCH** » Dom Nov 11, 2012 14:47

Sim caro colega...ajudou muito primeiro que me ensinou como colocar aqui e depois que por esta que me fez tentarei fazer outras, a unica coisa que ocorre é que uma é de somar ja a segunda de multiplicar ai eu ja fico perdida e pior tem com raiz ai eu nem sei colocar para me ajudarem e tem raiz dividida por outra raiz. mas a ajuda que me deu ja esta valendo demais obrigado. que a vida lhe dê as recompensas por ser assim como você é.

por **DanielFerreira** » Dom Nov 11, 2012 19:22

Silmara,
obrigado pelas palavras!
Para resolver o item b) você deverá efetuar o produto/multiplicação. Produto Notável.

Veja um exemplo:
(x + 1)(a + b) =
x.a + x.b + 1.a + 1.b =
ax + bx + a + b

'Sua' função:

$\\ f(x) = (x^2 - 2).(2x + 3) \\\\ f(x) = x^2 \cdot 2x + x^2 \cdot 3 - 2 \cdot 2x - 2 \cdot 3 \\\\ f(x) = 2x^3 + 3x^2 - 4x - 6$

Agora, vou deixar que termine!
E quero saber a resposta! :-D

Até logo!!

por **SILMARAKNETSCH** » Dom Nov 11, 2012 20:22

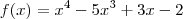
danjr5 escreveu:Silmara,
obrigado pelas palavras!
Para resolver o item b) você deverá efetuar o produto/multiplicação. Produto Notável.

Veja um exemplo:
(x + 1)(a + b) =
x.a + x.b + 1.a + 1.b =
ax + bx + a + b

'Sua' função:

$\\ f(x) = (x^2 - 2).(2x + 3) \\\\ f(x) = x^2 \cdot 2x + x^2 \cdot 3 - 2 \cdot 2x - 2 \cdot 3 \\\\ f(x) = 2x^3 + 3x^2 - 4x - 6$

Agora, vou deixar que termine!
E quero saber a resposta!

Até logo!!

tenho que fazer olhando no primeiro que me ajudou o f´(x) e tenho que entender la como vc fez para trabalhar com os expoentes

por **DanielFerreira** » Dom Nov 11, 2012 20:34

A grosso modo, o expoente 'desce' multiplicando e é substituído pelo seu antecessor.

por **SILMARAKNETSCH** » Dom Nov 11, 2012 20:45

SILMARAKNETSCH escreveu:
danjr5 escreveu:Silmara,
obrigado pelas palavras!
Para resolver o item b) você deverá efetuar o produto/multiplicação. Produto Notável.

Veja um exemplo:
(x + 1)(a + b) =
x.a + x.b + 1.a + 1.b =
ax + bx + a + b

'Sua' função:

$\\ f(x) = (x^2 - 2).(2x + 3) \\\\ f(x) = x^2 \cdot 2x + x^2 \cdot 3 - 2 \cdot 2x - 2 \cdot 3 \\\\ f(x) = 2x^3 + 3x^2 - 4x - 6$

Agora, vou deixar que termine!

f'´(x) = 2(.x)³-¹ + 3.(x)²-¹ - 4.(x)¹-¹ -6
f´(X) = 2.x² + 3x¹ - 4 - 6
f´(x) = 2x² + 3x¹ - 10
falta algo?

E quero saber a resposta!

Até logo!!

assim tenho tudo para aprender pois fui começando a enxergar de onde vem e onde por mas minha prova será sábado tenho que saber até lá. senão vou reprovar no bimestre

por **SILMARAKNETSCH** » Dom Nov 11, 2012 20:49

danjr5 escreveu:A grosso modo, o expoente 'desce' multiplicando e é substituído pelo seu antecessor.

esta me fazendo entender agora sai do rio afogando e comecei a dar as primeiras braçadas.

por **DanielFerreira** » Qua Nov 14, 2012 23:28

Continue com as braçadas e o objetivo será alcançado!

derivação de funções

derivação de funções

derivação de funções

Re: derivação de funções

Re: derivação de funções

Re: derivação de funções

Re: derivação de funções

Re: derivação de funções

Re: derivação de funções

Re: derivação de funções

Re: derivação de funções

Re: derivação de funções

Quem está online