Amigos e se possível Young Jedi.
Gostaria de obter a formula de uma curva S que define em termos de uma função f (x) = alguma coisa . x ou melhor y = alguma coisa . x os seguintes pares ordenados (x,y)
Se ajudar ... A curva S é uma exponencial até certo ponto até que a declividade muda. Forma um S como a curva Sigmoide.
ponto 1 - (1;0,41%)
ponto 2 - (2;0,67%)
ponto 3 - (3;1,10%)
ponto 4 - (4; 1,80%)
ponto 5 -(5;2,93%)
ponto 6 - (6;4,74%)
ponto 7 -(7;7,59%)
ponto 8 -(8;11,92%)
ponto 9 - (9;18,24%)
ponto 10 - (10;26,89%)
ponto 11 -(11;37,75%)
ponto12 - (12;50%)
ponto 13 ( 13;62,25%)
ponto 14 (14;73,11%)
ponto 15 (15;81,76%)
ponto 16 (16;88,08%)
ponto 17 (17;92,41%)
ponto 18 (18;95,26%)
ponto 19 (19;97,07%)
ponto 20 (20;98,20%)
ponto 21 (21;98,90%)
ponto 22 (22;99,33%)
ponto 23 (23;99,59%)
ponto 24 (24;99,75%)




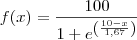



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)