 por JU201015 » Seg Nov 12, 2012 22:06
por JU201015 » Seg Nov 12, 2012 22:06
O produto das raízes da equação
![{3}^{x}+\frac{1}{{3}^{x}}=\frac{\sqrt[2]{3}}{3} {3}^{x}+\frac{1}{{3}^{x}}=\frac{\sqrt[2]{3}}{3}](/latexrender/pictures/b9c5600ed9d637557985cf0058f75209.png)
é?
Essa matéria realmente não entra na minha cabeça! Estou tentando praticar resolvendo exercícios, mas tem uns que eu realmente não consigo. Por favor, me ajudem?
-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Seg Nov 12, 2012 23:10
por MarceloFantini » Seg Nov 12, 2012 23:10
Vamos reescrever o lado direito como
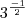
. Multiplicando tudo por

temos

. Faça a substituição

, daí

. Escrevendo
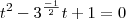
.
O produto das raízes desta equação é dado por

, que usando os coeficientes é igual a 1.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por JU201015 » Ter Nov 13, 2012 09:08
por JU201015 » Ter Nov 13, 2012 09:08
MarceloFantini escreveu:Vamos reescrever o lado direito como
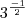
. Multiplicando tudo por

temos

. Faça a substituição

, daí

. Escrevendo
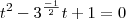
.
O produto das raízes desta equação é dado por

, que usando os coeficientes é igual a 1.
Mto obrigado!
-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Potenciação e Radiciação
por Carlos22 » Qua Abr 13, 2011 22:06
- 1 Respostas
- 1926 Exibições
- Última mensagem por FilipeCaceres

Qua Abr 13, 2011 22:27
Logaritmos
-
- [Potenciação e radiciação]
por SCHOOLGIRL+T » Qua Nov 07, 2012 21:19
- 4 Respostas
- 2663 Exibições
- Última mensagem por SCHOOLGIRL+T

Sex Nov 09, 2012 23:44
Álgebra Elementar
-
- Potenciação e radiciação
por anneliesero » Sáb Abr 27, 2013 22:46
- 1 Respostas
- 1662 Exibições
- Última mensagem por e8group

Sáb Abr 27, 2013 23:48
Álgebra Elementar
-
- Potenciação e radiciação
por anneliesero » Sáb Abr 27, 2013 22:51
- 1 Respostas
- 1250 Exibições
- Última mensagem por young_jedi

Dom Abr 28, 2013 21:20
Álgebra Elementar
-
- Potenciação e radiciação
por anneliesero » Sáb Abr 27, 2013 22:53
- 1 Respostas
- 1133 Exibições
- Última mensagem por nakagumahissao

Dom Abr 28, 2013 02:42
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![{3}^{x}+\frac{1}{{3}^{x}}=\frac{\sqrt[2]{3}}{3} {3}^{x}+\frac{1}{{3}^{x}}=\frac{\sqrt[2]{3}}{3}](/latexrender/pictures/b9c5600ed9d637557985cf0058f75209.png) é?
é?
![{3}^{x}+\frac{1}{{3}^{x}}=\frac{\sqrt[2]{3}}{3} {3}^{x}+\frac{1}{{3}^{x}}=\frac{\sqrt[2]{3}}{3}](/latexrender/pictures/b9c5600ed9d637557985cf0058f75209.png) é?
é?
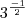 . Multiplicando tudo por
. Multiplicando tudo por  temos
temos  . Faça a substituição
. Faça a substituição  , daí
, daí  . Escrevendo
. Escrevendo 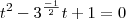 .
. , que usando os coeficientes é igual a 1.
, que usando os coeficientes é igual a 1.

. Multiplicando tudo por
temos
. Faça a substituição
, daí
. Escrevendo
.
, que usando os coeficientes é igual a 1.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
