Para resolver este limite:
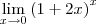
Basta colocar a resposta?
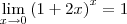
Meu professor falou q tenho q justificar minha resposta... mas justificar o que? Que x tende a zero, e como o número entre parênteses é um número real, o limite é 1? É isso ou há outra justificativa
ou por exemplo, se eu fosse calcular o limite abaixo:
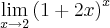 =
=  = 25
= 25Está certo?
Minha dúvida é pq está elevado a x, daí não sei se posso fazer isso.


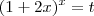 como a base não é fixa , vamos estabelecer um intervalo
como a base não é fixa , vamos estabelecer um intervalo  para
para  . Isso nos garante que
. Isso nos garante que  logo podemos dizer que
logo podemos dizer que  , logo
, logo 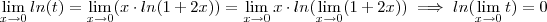 . Disso concluímos que ,
. Disso concluímos que , 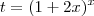 tende a um .
tende a um .

 .
.
 :
: