 por JU201015 » Sáb Nov 10, 2012 20:28
por JU201015 » Sáb Nov 10, 2012 20:28
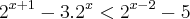
Me ajudem a resolver?
Ah! Eu tentei fazer esta e não deu nenhum resultado real. Isso é possível?
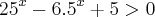
Bom, estou aprendendo essa matéria de equação exponencial e, mesmo eu sabendo as propriedades, tenho muita dúvida e não consigo fazer isso na prática. Queria que vcs me dessem exemplos e alguns modos de resolução se possível. Obg.
-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Sáb Nov 10, 2012 20:54
por young_jedi » Sáb Nov 10, 2012 20:54
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por MarceloFantini » Sáb Nov 10, 2012 21:02
por MarceloFantini » Sáb Nov 10, 2012 21:02
Ju, mantenha tópicos separados para dúvidas diferentes. Em outras palavras, crie um novo tópico para a segunda inequação.
Para a primeira, multiplique tudo por

e faça a substituição

. Então
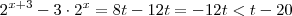
e

, logo
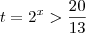
. Aplicando o logaritmo na base 2, temos
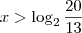
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por JU201015 » Sáb Nov 10, 2012 23:51
por JU201015 » Sáb Nov 10, 2012 23:51
Mto obrigado!

-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por JU201015 » Sáb Nov 10, 2012 23:53
por JU201015 » Sáb Nov 10, 2012 23:53
MarceloFantini escreveu:Ju, mantenha tópicos separados para dúvidas diferentes. Em outras palavras, crie um novo tópico para a segunda inequação.
Para a primeira, multiplique tudo por

e faça a substituição

. Então
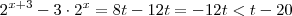
e

, logo
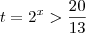
. Aplicando o logaritmo na base 2, temos
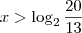
.
Podexá q não coloco mais dúvidas diferentes no mesmo tópico

Ah! E obrigado por responder minhas perguntas!
-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação exponencial???
por azheng » Sáb Nov 21, 2009 19:47
- 0 Respostas
- 1625 Exibições
- Última mensagem por azheng

Sáb Nov 21, 2009 19:47
Álgebra Elementar
-
- Equação Exponencial
por Adriana Baldussi » Seg Nov 23, 2009 14:41
- 3 Respostas
- 2838 Exibições
- Última mensagem por Molina

Seg Nov 23, 2009 17:07
Álgebra Elementar
-
- Equação Exponencial
por LeonardoSantos » Ter Fev 16, 2010 14:11
- 1 Respostas
- 2828 Exibições
- Última mensagem por Douglasm

Ter Fev 16, 2010 15:46
Funções
-
- Equação exponencial
por cristina » Sex Jun 04, 2010 20:19
- 1 Respostas
- 2241 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 00:27
Sistemas de Equações
-
- Equação exponencial
por nan_henrique » Sáb Jul 10, 2010 13:00
- 1 Respostas
- 2191 Exibições
- Última mensagem por Douglasm

Sáb Jul 10, 2010 13:12
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
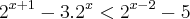
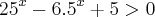


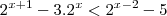
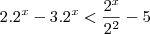
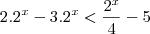

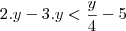
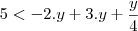
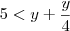
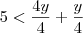
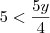
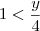

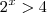
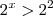


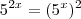

 e faça a substituição
e faça a substituição  . Então
. Então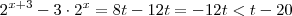
 , logo
, logo 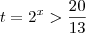 . Aplicando o logaritmo na base 2, temos
. Aplicando o logaritmo na base 2, temos 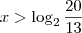 .
.



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.