 por SILMARAKNETSCH » Sáb Nov 10, 2012 11:20
por SILMARAKNETSCH » Sáb Nov 10, 2012 11:20
saiu quase perfeito só não consegui colocar o x flexinha infinito abaixo do lim - alguem poderia me ajudar a solucionar este exercício com etapas para eu aprender de fato?
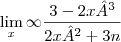
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
 por SILMARAKNETSCH » Sáb Nov 10, 2012 11:29
por SILMARAKNETSCH » Sáb Nov 10, 2012 11:29
porque apareceu este  se eu não os coloquei na fórmula?
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
 por MarceloFantini » Sáb Nov 10, 2012 14:50
por MarceloFantini » Sáb Nov 10, 2012 14:50
O código para este limite Silmara é
- Código: Selecionar todos
\lim_{x \to + \infty} \frac{3 - 2x^3}{2x^2 +3x}
assumindo que aquele

na verdade era um

. Aquele A provavelmente apareceu porque você quis usar o comando do teclado para texto normal, que escreveria x³, porém no LaTeX ele sai assim:
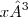
.
Sobre a resolução, quando temos divisão de dois polinômios o método mais usado em limites infinitos é colocar a maior potência de cada polinômio em evidência e perceber o resultado da divisão. Neste caso teremos
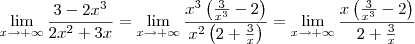
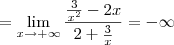
.
Para entender o resultado, lembre-se que
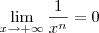
e que

, ou seja, que podemos retirar uma constante multiplicando o limite.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por SILMARAKNETSCH » Sáb Nov 10, 2012 15:55
por SILMARAKNETSCH » Sáb Nov 10, 2012 15:55
MUITO GRATA MARCELO, VOU TROCAR NÚMEROS E TREINAR TEEI PROVA NO FINAL DO MES E UM COLEGA DE VOVES ME ENSINOU QUE DEVO FAZER EXERCICIOS E TREINANDO ASSIM APRENDO, MAIS UMA VEZ MINHA GRANDE GRATIDÃO.
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
 por MarceloFantini » Sáb Nov 10, 2012 16:13
por MarceloFantini » Sáb Nov 10, 2012 16:13
Trocar números não é sempre a melhor forma de aprender. No máximo ele te ensina que os números não importam. Fixe-se nos conceitos, eles resolverão qualquer exercício.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por SILMARAKNETSCH » Sáb Nov 10, 2012 16:21
por SILMARAKNETSCH » Sáb Nov 10, 2012 16:21
MarceloFantini escreveu:Trocar números não é sempre a melhor forma de aprender. No máximo ele te ensina que os números não importam. Fixe-se nos conceitos, eles resolverão qualquer exercício.
OK OBRIGADO POR MAIS ESTE ENSINO
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6646 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4793 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5121 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7263 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4440 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
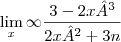


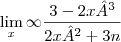


 na verdade era um
na verdade era um  . Aquele A provavelmente apareceu porque você quis usar o comando do teclado para texto normal, que escreveria x³, porém no LaTeX ele sai assim:
. Aquele A provavelmente apareceu porque você quis usar o comando do teclado para texto normal, que escreveria x³, porém no LaTeX ele sai assim: 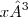 .
.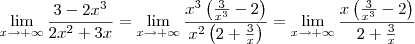
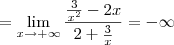 .
.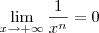 e que
e que  , ou seja, que podemos retirar uma constante multiplicando o limite.
, ou seja, que podemos retirar uma constante multiplicando o limite.




