Olá, estou com muita dificuldade pra poder montar o raciocínio desta questão...
consigo resolvê-la de forma cursiva, trabalhosa... por extenso... e no vestibular
não posso perder tanto tempo procurando uma resposta que uma expressão
simplesmente me responderá... por favor me ajudem.. obrigado...
Para um passeio em uma lancha, com capacidade para 60 pessoas, uma empresa de turismo
cobra R$80,00 por pessoa quando todos os lugares estão ocupados. Caso existam lugares
não ocupados, ao preço de cada passagem será acrescida a importância de R$2,00 por lugar não ocupado.
Para que a empresa tenha faturamento máximo com esse passeio, pode-se afirmar que o número
de lugares não ocupados na lancha é igual a:
01) 20
02) 17
03) 15
04) 13
05) 10 (resposta correta)
60 lugares -> 80,00 por pessoa -> 4.800 reais totalizados
\/ 60p | 80r | 4800 /\
\/ 59p | 80+2 | 4828 /\
\/ 58p | 80+4 | 4872 /\
--> tentei me expressar por : (60-x).(80+2x)= 4800+ ?
_____________________________________________________
_____________________________________________________


 , esta função .
, esta função .  se x = 60
se x = 60  o números de lugares não ocupados assim ,
o números de lugares não ocupados assim ,  .
.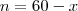
 = 200x -2x^2 ; x < 60 \end{cases} p(x) = \begin{cases} 60 \cdot 80 ; x = 60 \\ [80 + 2(60-x)](x) = 200x -2x^2 ; x < 60 \end{cases}](/latexrender/pictures/c715317fc6c2b4476d507758325f1bc4.png)
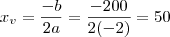 Este ponto fornecerá o valor máximo de p(x) , pois a concavidade estar voltada para baixo .
Este ponto fornecerá o valor máximo de p(x) , pois a concavidade estar voltada para baixo .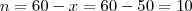

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
