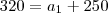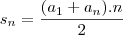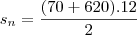por joedsonazevedo » Sex Nov 09, 2012 11:49
por joedsonazevedo » Sex Nov 09, 2012 11:49
Olá, a questão que estou desenvolvendo é a seguinte...
Uma revendedora de automóveis observou que, em determinado ano, a venda de veículos automáticos aumentava, mensalmente, segundo uma progressão aritmética de razão 50. Considerando-se que, em junho, foram vendidas
320 unidades, pode se afirmar que o numero de veículos automáticos comercializados pela revendedora,
nesse ano, foi igual a
01) 690
02) 1380
03) 2070
04) 4140
05) 8280
Resolvi da seguinte forma:
(r= 50) (a6= 320) (a12 e a1= ?)
descobrindo a12 pela formula geral
--> an = a1 + (n+1)r
a6 = a12 +(6-12).50
320 = a12 - 300
a12= 620
descobrindo a1:
a6 = a1 + (6-1).50
320 = a1 + 250
a1 = 30
Utilizei a formula da Soma de termos para saber a soma
dos valores de carros vendidos nos 12 meses...
--> Sn = (a1+an).n => (30+620).12 => Sn = 3900
..............2.................2
porém não confere com o resultado do gabarito... que é 4140
gostaria de ajuda na interpretação da questão ou no próprio cálculo...
______________________________________________Muito Obrigado!
______________________________________________Joedson Azevedo
____________________________________________________________
-
joedsonazevedo
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qui Nov 08, 2012 14:23
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. em Informática
- Andamento: formado
 por young_jedi » Sex Nov 09, 2012 15:29
por young_jedi » Sex Nov 09, 2012 15:29
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UNIFOR) Progressão Aritmética e Progressão Harmônica
por andersontricordiano » Ter Mar 22, 2011 12:56
- 1 Respostas
- 6132 Exibições
- Última mensagem por LuizAquino

Ter Mar 22, 2011 13:52
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4724 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- [Aritmética] Progressão Aritmética.
por Pessoa Estranha » Qua Ago 28, 2013 22:11
- 2 Respostas
- 5629 Exibições
- Última mensagem por Pessoa Estranha

Qui Ago 29, 2013 16:06
Aritmética
-
- Progressão Aritmética
por Rejane Sampaio » Qua Set 17, 2008 16:20
- 1 Respostas
- 4422 Exibições
- Última mensagem por juliomarcos

Qui Set 18, 2008 13:07
Álgebra Elementar
-
- Progressão Aritmética (PA)
por Cleyson007 » Ter Jan 27, 2009 21:40
- 2 Respostas
- 8395 Exibições
- Última mensagem por Cleyson007

Sáb Mai 30, 2009 12:31
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.