 por SCHOOLGIRL+T » Qua Nov 07, 2012 20:53
por SCHOOLGIRL+T » Qua Nov 07, 2012 20:53
(UFMG) Nessa figura, estão representados os gráficos das funções f(x) = x²/2 e g(x) = 3x - 5.

Considere os segmentos paralelos ao eixo y, com uma das extremidades sobre o gráfico da função f e a outra extremidade sobre o gráfico da função g. Entre esses segmentos, seja S o que tem o menor comprimento. Assim sendo, o comprimento do segmento S é
a) 1/2 b) 3/4 c) 1 d) 5/4
Me ajudem passo a passo? Obg.
-
SCHOOLGIRL+T
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Nov 07, 2012 08:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Qui Nov 08, 2012 16:13
por young_jedi » Qui Nov 08, 2012 16:13
se o segmento é paralelo ao eixo y então nos temos que para qualquer ponto do sgmento o valor de x é o memso para qualquer ponto do segmento
então o comprimento do segmento é dado por
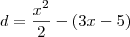
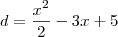
percebmeos que o comprimento esta em função de x e que ieta é uma função do segundo grau,
vemos tambem que o coeficiente a da equação é positivo portanto é uma parabola com a concavidade voltada para cima, sendo assim seu valor minimo esta no vertice desta parabola.
portanto calculando o vertice
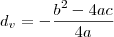
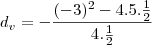
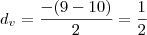
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por SCHOOLGIRL+T » Qui Nov 08, 2012 20:17
por SCHOOLGIRL+T » Qui Nov 08, 2012 20:17
young_jedi escreveu:se o segmento é paralelo ao eixo y então nos temos que para qualquer ponto do sgmento o valor de x é o memso para qualquer ponto do segmento
então o comprimento do segmento é dado por
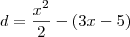
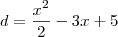
percebmeos que o comprimento esta em função de x e que ieta é uma função do segundo grau,
vemos tambem que o coeficiente a da equação é positivo portanto é uma parabola com a concavidade voltada para cima, sendo assim seu valor minimo esta no vertice desta parabola.
portanto calculando o vertice
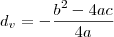
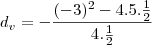
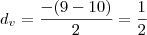
Obg^^ Fazia tempo que eu estava procurando a resolução desta questão, que continuo não entendendo muito kk Mas vc foi qm melhor me explicou...
-
SCHOOLGIRL+T
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Nov 07, 2012 08:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funções - Questão UFMG
por Larissa Valim » Dom Fev 24, 2013 16:12
- 2 Respostas
- 2769 Exibições
- Última mensagem por Russman

Dom Fev 24, 2013 19:23
Funções
-
- Questão UFMG
por Guilherme Carvalho » Qui Mar 03, 2011 13:03
- 1 Respostas
- 4778 Exibições
- Última mensagem por Elcioschin

Qui Mar 03, 2011 13:27
Álgebra Elementar
-
- Questão da UFMG
por Kelvin Brayan » Sáb Mar 12, 2011 17:19
- 1 Respostas
- 5011 Exibições
- Última mensagem por Rogerio Murcila

Qua Mar 16, 2011 23:42
Matemática Financeira
-
- Questão da UFMG
por Kelvin Brayan » Dom Mar 13, 2011 16:26
- 4 Respostas
- 2644 Exibições
- Última mensagem por Kelvin Brayan

Seg Mar 14, 2011 00:34
Cálculo: Limites, Derivadas e Integrais
-
- Questão UFMG
por Guilherme Carvalho » Qua Mar 16, 2011 16:39
- 5 Respostas
- 3061 Exibições
- Última mensagem por Kelvin Brayan

Ter Mar 22, 2011 00:23
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



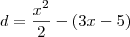
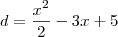
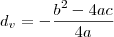
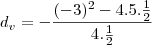
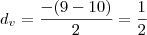

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
