 por manuoliveira » Qua Nov 07, 2012 15:26
por manuoliveira » Qua Nov 07, 2012 15:26
Dado T: R³ -> R³ ; T(x1, x2, x3) = (3.x1 + x2, - 2.x1 - 4.x2 + 3.x3, 5.x1 + 4.x2 - 2.x3), A e B bases canônicas, encontrar T^(-1)(v)
Gente, tenho prova amanhã e estou toda enrolada com essa parte, não estou conseguindo achar a inversa de nenhuma questão, agradeço muito quem puder me ajudar com essa! Obrigadinha

-
manuoliveira
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qui Abr 01, 2010 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por young_jedi » Qua Nov 07, 2012 21:23
por young_jedi » Qua Nov 07, 2012 21:23
tome que a transformação (x1,x2,x3) leva a (a,b,c)

portanto
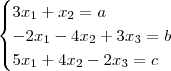
isolando x2 na primeira equação temos que

substituindo na segunda e terceira equações
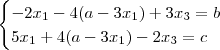
isolando x3 na primeria das equações acima

substituindo na segunda equação
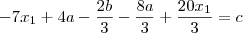
isolando x1

substituindo este valor de x1 na equação de x3


substituindo o valor de x1 na equação de x2


portanto
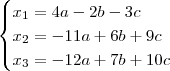
sendo assim
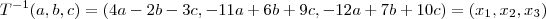
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por manuoliveira » Qua Nov 07, 2012 22:23
por manuoliveira » Qua Nov 07, 2012 22:23
Nossa... obrigada, obrigada, obrigada mesmoooo!!!
-
manuoliveira
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qui Abr 01, 2010 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Transformação Linear] Nucleo e Imagem, ache a transformaçao
por vualas » Qua Nov 07, 2012 00:37
- 2 Respostas
- 4248 Exibições
- Última mensagem por adauto martins

Qui Dez 15, 2016 11:12
Álgebra Linear
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 10527 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- Álgebra Linear -Transformação linear- Isomorfismo
por anapaulasql » Ter Jan 27, 2015 22:08
- 1 Respostas
- 11559 Exibições
- Última mensagem por adauto martins

Ter Mar 29, 2016 13:15
Álgebra Linear
-
- [Álgebra Linear] Transformação Linear Idenpotente
por Zubumafu67 » Ter Nov 17, 2020 11:38
- 0 Respostas
- 13598 Exibições
- Última mensagem por Zubumafu67

Ter Nov 17, 2020 11:38
Álgebra Linear
-
- [Álgebra Linear] Transformação linear
por Debby » Dom Mai 27, 2012 12:17
- 2 Respostas
- 9139 Exibições
- Última mensagem por Debby

Dom Mai 27, 2012 20:27
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





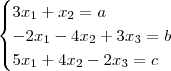

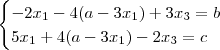

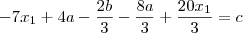





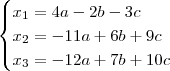
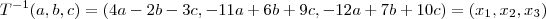


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.