 por SCHOOLGIRL+T » Qua Nov 07, 2012 09:38
por SCHOOLGIRL+T » Qua Nov 07, 2012 09:38
Considere as desigualdades ax + bx + c > 0, em que a, b e c são números reais. Sabe-se que x= -62/7 e x= 7/25 satisfazem essa desigualdade; e x= -42 e x=26/25 não a satisfazem. Assim sendo, é correto afirmar que:
a) b>0
b) b² - 4ac >0
c) c<0
d) a>0
Me expliquem passo a passo? Obg.
-
SCHOOLGIRL+T
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Nov 07, 2012 08:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Qua Nov 07, 2012 12:08
por young_jedi » Qua Nov 07, 2012 12:08
note que se temos uma função
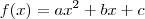
seu grafico é uma parabola
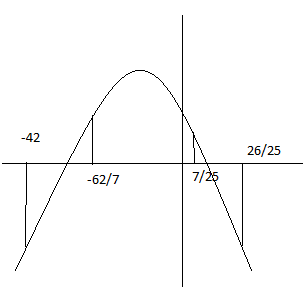
- desmonstração.png (4.74 KiB) Exibido 621 vezes
pelo fato de
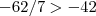
e
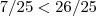
sabemos que ela é uma parabaloa voltada para baixo (a<0) e que esta função corta o eixo x em dois pontos, portanto ela tem duas raizes reais, mais para que ela tenha duas raizes reais é necessario que
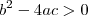
portanto esta é a afirmação correta
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Funções] AJUDA, FUNÇÃO QUADRÁTICA ( UnB ).
por alziroMS » Qui Ago 02, 2012 12:27
- 1 Respostas
- 1182 Exibições
- Última mensagem por alziroMS

Sáb Ago 04, 2012 00:05
Funções
-
- Função quadrática
por Ananda » Sex Mar 28, 2008 16:00
- 6 Respostas
- 9243 Exibições
- Última mensagem por admin

Sex Mar 28, 2008 21:25
Funções
-
- Função quadratica
por Aline » Qui Jun 18, 2009 14:22
- 2 Respostas
- 2634 Exibições
- Última mensagem por Cleyson007

Sex Jun 19, 2009 10:00
Funções
-
- Função Quadratica
por Aline » Qui Jun 18, 2009 14:37
- 1 Respostas
- 2018 Exibições
- Última mensagem por Marcampucio

Qui Jun 18, 2009 16:45
Funções
-
- Função Quadratica
por Aline » Sáb Jun 20, 2009 18:23
- 1 Respostas
- 2097 Exibições
- Última mensagem por Molina

Dom Jun 21, 2009 20:28
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


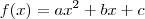
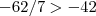 e
e 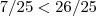 sabemos que ela é uma parabaloa voltada para baixo (a<0) e que esta função corta o eixo x em dois pontos, portanto ela tem duas raizes reais, mais para que ela tenha duas raizes reais é necessario que
sabemos que ela é uma parabaloa voltada para baixo (a<0) e que esta função corta o eixo x em dois pontos, portanto ela tem duas raizes reais, mais para que ela tenha duas raizes reais é necessario que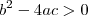


 .
.



